K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

24 tháng 11 2023
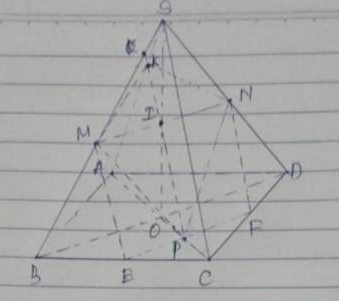
1: Gọi giao điểm của AC và BD là O trong mp(ABCD)
\(O\in AC\subset\left(SAC\right)\)
\(O\in BD\subset\left(SBD\right)\)
Do đó: \(O\in\left(SAC\right)\cap\left(SBD\right)\)
mà \(S\in\left(SAC\right)\cap\left(SBD\right)\)
nên (SAC) giao (SBD)=SO
Xét ΔSDC có
P,N lần lượt là trung điểm của DS,DC
=>PN là đường trung bình của ΔSDC
=>PN//SC
PN//SC
SC\(\subset\)(SBC)
PN không nằm trong mp(SBC)
Do đó: PN//(SBC)


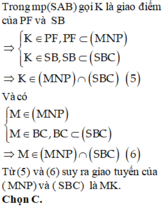
a:
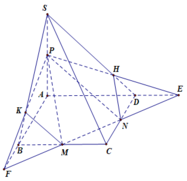
1: \(M\in SB\subset\left(SAB\right)\)
\(M\in\left(MNP\right)\)
Do đó: \(M\in\left(SAB\right)\cap\left(MNP\right)\)(1)
\(N\in AB\subset\left(SAB\right)\)
\(N\in\left(MNP\right)\)
Do đó: \(N\in\left(SAB\right)\cap\left(MNP\right)\left(2\right)\)
Từ (1),(2) suy ra \(\left(SAB\right)\cap\left(MNP\right)=MN\)
2:
\(M\in SB\subset\left(SBC\right);M\in\left(MNP\right)\)
=>\(M\in\left(SBC\right)\cap\left(MNP\right)\)(3)
\(P\in BC\subset\left(SBC\right);P\in\left(MNP\right)\)
=>\(P\in\left(SBC\right)\cap\left(MNP\right)\)(4)
Từ (3),(4) suy ra \(\left(SBC\right)\cap\left(MNP\right)=MP\)
3:
\(N\in AB\subset\left(ABC\right);N\in\left(MNP\right)\)
=>\(N\in\left(ABC\right)\cap\left(MNP\right)\)(5)
\(P\in BC\subset\left(ABC\right);P\in\left(MNP\right)\)
=>\(P\in\left(ABC\right)\cap\left(MNP\right)\left(6\right)\)
Từ (5),(6) suy ra \(\left(ABC\right)\cap\left(MNP\right)=NP\)
b: Xét ΔBAS có BN/BA=BM/BS
nên NM//AS
=>MN//(SAC)