Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

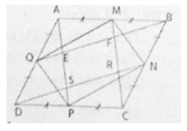
a) Ta có AB // CD (gt)
Suy ra AM // CP (1)
Lại có AM = AB/2; CP = CD/2 (2)
Từ (1) và (2) suy ra AMCP là hình bình hành
Suy ra AP // CM hay ES // FR.
Tương tự ta cũng chứng minh được tứ giác BQDN là hình bình hành nên BQ // DN. Suy ra EF // RS.
Vậy tứ giác EFRS là hình bình hành
b) Đặt PS = x. Suy ra CR = 2x (tính chất đường trung bình)
Từ đó suy ra RF = ES = AE = 2x
Suy ra: ES = 2AP/5 => SEFRS = 2SAMCP/5
Vì SAMCP = SABCD/2 nên SEFRS = SABCD/2

( bạn tự vẽ hình nha )
a, Vì M nằm tren cạnh AB, N nằm trêm cạnh CD => AM \(//\) CN
Mà AM=CN ( Theo gt) . Do đó tứ giác AMCN là hình bình hành ( Theo đk 3)
b, Vì ABCD là hình bình hành => Góc A= Góc C
Xét 2 tam giác AMP và tam giác CNQ bằng nhau theo TH c-g-c ( Tự CM )
=> MP=NC( 2 cạnh tương ứng )(1)
CMTT 2 tam giác MBQ và NDP ta được MQ=PN (2)
Từ (1) và (2) ta có MPNQ là hình bình hành (đpcm)
 học tốt
học tốt Học tốt
Học tốt
Giải: Xét tam giác ACD có F,G lần lượt là trung điểm AC,DC nên FG là đường trung bình
⇒⇒FG//ADFG//AD
C/m tương tự đc EH//AD;GH//EF//BCEH//AD;GH//EF//BC
⇒EFGH⇒EFGH là hình bình hành
a/Để EFGH là hình chữ nhật thì góc FGH=90oFGH=90o
⇒gócHGD+gócFGC=90o⇒gócHGD+gócFGC=90o
Mà góc HGD=góc BCD;góc FGC= góc ADC ( góc đồng vị = nhau)
⇒⇒ góc BCD+góc ADC=90o90o
⇒⇒Để EFGH là hình chữ nhật thì tứ giác ABCD cần có góc BCD+góc ADC=90o90o
b/Để EFGH là hình thoi thì FG=HG
Mà FG=1/2AD; HG=1/2BC
⇒⇒AD=BC
⇒⇒Để EFGH là hình thoi thì tứ giác ABCD có AD=BC
c/ để EFGH là hình vuông thì EFGH phải vừa là hình chữ nhật vừa là hình thoi⇒⇒ABCD phải có đủ cả hai điều kiện trên
Nối A với C ta có AP là đường trung tuyến của ΔACDΔACD nên
SADP=SAPC=12SADC=14SABCDSADP=SAPC=12SADC=14SABCD
Tương tự SACR=SBCR=12SABC=14SABCD.SACR=SBCR=12SABC=14SABCD.
⇒SAPC+SACR=SARCP=12SABCD.⇒SAPC+SACR=SARCP=12SABCD.
SADP=SAPC=12SADC=14SABCDSADP=SAPC=12SADC=14SABCD
Tương tự SACR=SBCR=12SABC=14SABCD.SACR=SBCR=12SABC=14SABCD.
⇒SAPC+SACR=SARCP=12SABCD.⇒SAPC+SACR=SARCP=12SABCD.
Gọi H là giao điểm của AP và BQ, K là giao điểm của CR và BQ, M là giao điểm của AP và DS, N là giao điểm của CR và DS.
Dễ thấy HKNM là hình bình hành nên các tam giác sau đây có cùng diện tích:
SAKH=SHKM=SMNH=SMNCSAKH=SHKM=SMNH=SMNC=SAKB=SMCD=SAKB=SMCD
Mà SAKR=12SAKBSAKR=12SAKB (đáy gấp đôi, chung đường cao)
Tương tự SMPC=12SMCDSMPC=12SMCD
⇒SAKH=SHKM=SMNH⇒SAKH=SHKM=SMNH=SMNC=(SAKR+SMPC)=SMNC=(SAKR+SMPC)=15SARCP.=15SARCP.
Mà SARCP=12SABCDSARCP=12SABCD
⇒SHKM+SMKN=15SABCD⇒SHKM+SMKN=15SABCD hay SKHMN=15SABCD.