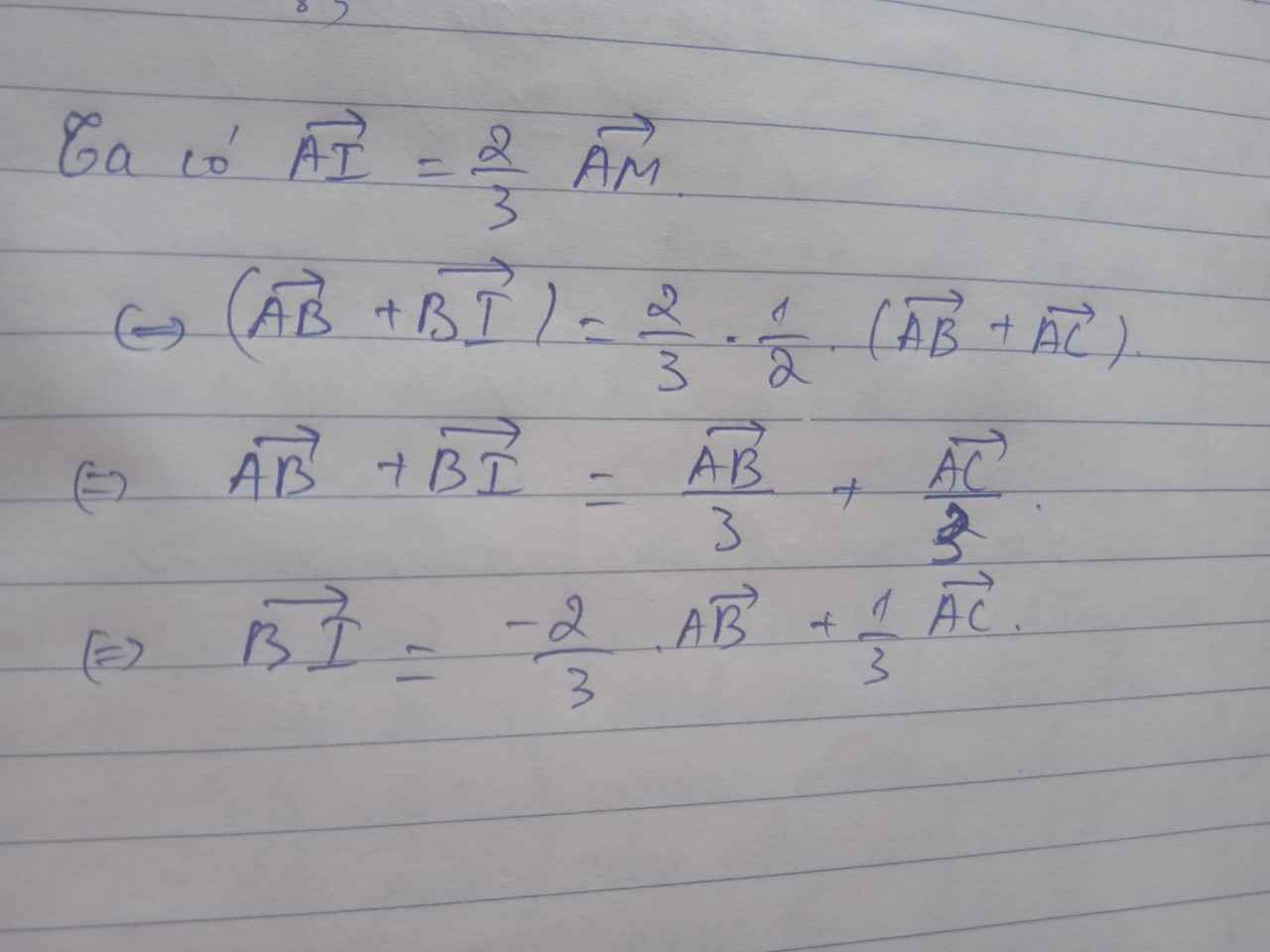Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: CI+BI=CB
=>\(\dfrac{3}{2}BI+BI=CB\)
=>\(\dfrac{5}{2}BI=CB\)
=>\(BI=\dfrac{2}{5}BC\)
=>\(CI=\dfrac{3}{2}\cdot BI=\dfrac{3}{2}\cdot\dfrac{2}{5}CB=\dfrac{3}{5}CB\)
\(\overrightarrow{AI}=\overrightarrow{AB}+\overrightarrow{BI}\)
\(=\overrightarrow{AB}+\dfrac{2}{5}\overrightarrow{BC}\)
\(=\overrightarrow{AB}+\dfrac{2}{5}\overrightarrow{BA}+\dfrac{2}{5}\overrightarrow{AC}\)
\(=\dfrac{3}{5}\overrightarrow{AB}+\dfrac{2}{5}\overrightarrow{AC}\)
JB=2/5JC mà J không nằm trong đoạn thẳng BC
nên B nằm giữa J và C
=>JB+BC=JC
=>\(BC+\dfrac{2}{5}JC=JC\)
=>\(BC=\dfrac{3}{5}JC\)
\(\dfrac{JB}{BC}=\dfrac{\dfrac{2}{5}JC}{\dfrac{3}{5}JC}=\dfrac{2}{5}:\dfrac{3}{5}=\dfrac{2}{3}\)
=>\(JB=\dfrac{2}{3}BC\)
\(\overrightarrow{AJ}=\overrightarrow{AB}+\overrightarrow{BJ}\)
\(=\overrightarrow{AB}-\dfrac{2}{3}\overrightarrow{BC}\)
\(=\overrightarrow{AB}-\dfrac{2}{3}\left(\overrightarrow{BA}+\overrightarrow{AC}\right)\)
\(=\overrightarrow{AB}-\dfrac{2}{3}\overrightarrow{BA}-\dfrac{2}{3}\overrightarrow{AC}=\dfrac{5}{3}\overrightarrow{AB}-\dfrac{2}{3}\overrightarrow{AC}\)
b:
Gọi giao điểm của AG với BC là M
G là trọng tâm của ΔABC
nên AG cắt BC tại trung điểm M của BC
=>\(AG=\dfrac{2}{3}AM\)
Xét ΔABC có AM là trung tuyến
nên \(\overrightarrow{AM}=\dfrac{1}{2}\left(\overrightarrow{AB}+\overrightarrow{AC}\right)\)
=>\(\overrightarrow{AG}=\dfrac{2}{3}\cdot\dfrac{1}{2}\left(\overrightarrow{AB}+\overrightarrow{AC}\right)=\dfrac{1}{3}\overrightarrow{AB}+\dfrac{1}{3}\overrightarrow{AC}\)
Đặt \(\overrightarrow{AG}=x\cdot\overrightarrow{AI}+y\cdot\overrightarrow{AJ}\)
\(\overrightarrow{AG}=\dfrac{1}{3}\cdot\overrightarrow{AB}+\dfrac{1}{3}\cdot\overrightarrow{AC};\overrightarrow{AI}=\dfrac{3}{5}\cdot\overrightarrow{AB}+\dfrac{2}{5}\cdot\overrightarrow{AC};\overrightarrow{AJ}=\dfrac{5}{3}\overrightarrow{AB}-\dfrac{2}{3}\cdot\overrightarrow{AC}\)
Ta có hệ phương trình sau:
\(\left\{{}\begin{matrix}\dfrac{1}{3}=x\cdot\dfrac{3}{5}+y\cdot\dfrac{5}{3}\\\dfrac{1}{3}=x\cdot\dfrac{2}{5}+y\cdot\dfrac{-2}{3}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x\cdot\dfrac{3}{5}+y\cdot\dfrac{5}{3}=\dfrac{1}{3}\\x\cdot\dfrac{2}{5}+y\cdot\dfrac{-2}{3}=\dfrac{1}{3}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}9x+25y=5\\6x-10y=5\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}18x+50y=10\\18x-30y=15\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}80y=-5\\6x-10y=5\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=-\dfrac{1}{16}\\6x=10y+5=-\dfrac{5}{8}+5=\dfrac{35}{8}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=-\dfrac{1}{16}\\x=\dfrac{35}{48}\end{matrix}\right.\)
Vậy: \(\overrightarrow{AG}=\dfrac{35}{48}\overrightarrow{AI}-\dfrac{1}{16}\overrightarrow{AJ}\)

Bài 1:
Gọi K là trung điểm của BC
ABCD là hình bình hành
=>AC cắt BD tại trung điểm của mỗi đường
=>O là trung điểm chung của AC và BD
Xét ΔCAB có
O,K lần lượt là trung điểm của CA,CB
=>OK là đường trung bình
=>OK//AB và \(OK=\dfrac{AB}{2}\)
=>\(\overrightarrow{OK}=\dfrac{\overrightarrow{AB}}{2}\)
=>\(\overrightarrow{AB}=2\cdot\overrightarrow{OK}\)
Xét ΔOBC có OK là đường trung tuyến
nên \(\overrightarrow{OB}+\overrightarrow{OC}=2\cdot\overrightarrow{OK}\)
=>\(\overrightarrow{AB}=\overrightarrow{OB}+\overrightarrow{OC}\)
=>M trùng với B
Bài 2:
Xét ΔABC có
M,P lần lượt là trung điểm của AB,AC
=>MP là đường trung bình của ΔABC
=>MP//BC và MP=BC/2
=>MP=CN
mà MP//NC
nên MPCN là hình bình hành
=>\(\overrightarrow{MP}=\overrightarrow{NC}\)
=>\(\overrightarrow{MP}=-\overrightarrow{CN}\)
=>\(\overrightarrow{MP}+\overrightarrow{CN}=\overrightarrow{0}\)
mà \(\overrightarrow{MK}+\overrightarrow{CN}=\overrightarrow{0}\)
nên K trùng với P

Câu 1:
vecto AM+vecto BN+vecto CP
=1/2(vecto AB+vecto AC+vecto BA+vecto BC+vecto CA+vecto CB)
=1/2*vecto 0
=vecto 0

\(\overrightarrow{AM}=\overrightarrow{AB}+\overrightarrow{BM}\)
\(=\overrightarrow{AB}+\dfrac{2}{3}\overrightarrow{BC}\)
\(=\overrightarrow{AB}+\dfrac{2}{3}\left(\overrightarrow{BA}+\overrightarrow{AC}\right)\)
\(=\dfrac{1}{3}\overrightarrow{AB}+\dfrac{2}{3}\overrightarrow{AC}\)