Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giải :
a) + K là trung điểm của AB ⇒ AK = \(\frac{AB}{2}\).
+ I là trung điểm của CD ⇒ CI = \(\frac{CD}{2}\).
+ ABCD là hình bình hành
⇒ AB // CD hay AK // CI
và AB = CD ⇒ AB/2 = \(\frac{CD}{2}\) hay AK = CI
+ Tứ giác AKCI có AK // CI và AK = CI
⇒ AKCI là hình bình hành.
b) + AKCI là hình bình hành
⇒ AI // KC hay \(\frac{MI}{NC}\).
\(a)\)
\(K\)là trung điểm \(AB\)\(\Rightarrow AK=\frac{AB}{2}\)
\(I\)là trung điểm \(CD\)\(\Rightarrow CI=\frac{CD}{2}\)
Mà theo đề ra: \(ABCD\)là hình bình hành
\(\Rightarrow AB//CD\)hay \(AK//CI\)
\(\Rightarrow AB=CD\Rightarrow\frac{AB}{2}=\frac{CD}{2}\)hay \(AK=CI\)
Tứ giác \(AKCI\)có \(AK//CI\)\(;\)\(AK=CI\)
\(\Rightarrow AKCI\)là hình bình hành
\(b)\)
Theo phần a), ta có: \(AKCI\)là hình bình hành
\(\Rightarrow AI//KC\)hay \(MI//NC\)
A K B N M I C D

a) + K là trung điểm của AB ⇒ AK = AB/2.
+ I là trung điểm của CD ⇒ CI = CD/2.
+ ABCD là hình bình hành
⇒ AB // CD hay AK // CI
và AB = CD ⇒ AB/2 = CD/2 hay AK = CI
+ Tứ giác AKCI có AK // CI và AK = CI
⇒ AKCI là hình bình hành.
b) + AKCI là hình bình hành
⇒ AI//KC hay MI//NC.
ΔDNC có: DI = IC, IM // NC ⇒ DM = MN (1)
+ AI // KC hay KN//AM
ΔBAM có: AK = KB, KN//AM ⇒ MN = NB (2)
Từ (1) và (2) suy ra DM = MN = NB.

a,ta có:tg ABCD là hình bình hành
AB song song DC
AK song song IC (1)
mà K là trung điểm của AB
AK=1/2AB
tương tự IK=1/2DC
mà AB=DC
AK=IC (2)
từ (1)và(2)suy ra tg AKCI là hbh
AI song song KC
Chỉ giải được 1 câu thôi thông cảm nhé
câu b:
Vì AI//KC=)IM//NC.Tam giác DNC có đoạn IM cắt trung điểm của DC và // với NC=)M là trung điểm DN=)DM=MN
làm tương tự với tam giác AMB
chỉ giải được câu 2 thôi thông cảm nhé

a)Xét hbh ABCD có:
AB//CD, AB=Cd(t/c)
K là tđ AB
I là tđ CD
=> AK=IC, AK//IC
=> AKCI là hbh(dhnb)
=> AI//KC(t/c)
b) Xét tam giác ABM:
K là tđ AB
KN//AM(M thuộc AI, N thuộc KC)
=> KN là đg tb
=> MN=MB (t/c) (1)
Xét t.giác DNC
I là tđ CD
IM//NC
=> IM là đg tb của t.giác DNC
=> MD=MN (t/c) (2)
(1),(2)=> DM= MN= NB

Ta có hình vẽ: A K B C I D M N
a) Ta có: AK = \(\dfrac{1}{2}\) AB
IC = \(\dfrac{1}{2}\) DC
mà AB = DC (vì ABCD là hình bình hành)
=> AK = IC
=> AK // IC (vì AB // DC)
=> AKCI là hình bình hành
=> AI // KC
b) Xét \(\Delta ABM\) có:
AK = KB (gt)
AM // KN (vì AI // KC)
=> BN = MN (1)
Xét \(\Delta DNC\) có:
DI = IC (gt)
IM // CN (vì AI // KC)
=> DM = MN (2)
từ (1) và (2) => DM = MN =NB

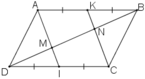
Cho hình bình hành ABCD. Gọi I,K theo thứ tự là trung điểm của CD, AB. Đường chéo BD cắt AI, CK theo thứ tự ở M và N. Chứng minh rằng:
a) AI // CK
b) DM = MN = NB


Kẻ đường chéo AC
có E,F,G,H theo thứ tự là trung điểm của các cạnh AB, BC, CD, DA
suy ra EF là đường trung bình của tam giác ABC nên EF//=1/2AC (1)
GH là đường trung bình của tam giác ADC nên GH//=1/2AC (2)
Từ (1) và (2) suy ra EF//=GH nên EFGH là hình bình hành
Vì có hai cạnh đối song song và bằng nhau
GOOD LUCK