Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C D F E O G H M P N
a) Gọi O là giao điểm của BD và AC
Theo bài ra ta có: \(BE=DF< \frac{BD}{2}\)
=> DF<DO và BF< BO
=> E nằm giữa B và O ;
F nằm giữa D và O
O là giao điểm 2 đường chéo của hình bình hành ABCD => OB=OD
Theo bài ra : EB = FD
=> OB-EB= OD-FD
=> OF=OE
Xét tứ giác AECF có: O là trung điểm EF ( OE=OF) và O là trung điểm AC ( ABCD là hình bình hành)
=> AECF là hình bình hành
b) G/s: AN =NM=MB => AM=2/3 AB
=> M là trọng tâm tam giác AGC
mà O là trung điểm AC
=> G; M; O thẳng hàng (1)
Gọi H là giao điểm của CM và AG
=> H là trung điểm AG ,
Lấy P là trung điểm GM
=> HP là đường trung bình của tam giác GAM
=> HP// = 1/2 AM
=> HP//= MB
=> HPBM là hình bình hành
=> PB//=HM
=> PB //ME
Xét tam giác OPB có PB//ME ; M là trung điểm OP
=> ME là đường trung bình
=> E là trung điểm OB
Vậy E là trung điểm OB với O là giao điểm của hai đường chéo hình bình hành ABCD

Ta có:
tam giác AEB = tam giác CFD
=> \(\widehat{AEB}=\widehat{CFD}=\widehat{EDF}\left(slt\right)\)
mà 2 goác có vị trí đồng vị
=> EB//DF
Mặt khác: ED//BF
=> EBFD là h.b.h
Ta có:
Tam giác END= tam giác FMB
=> DN=BM
=> DN+MN=BM+MN=BN
Ta có:
Vì tứ giác ABCD và EBFC đều là h.b.h
=> AC, BD, EF đồng quy tại trung điểm của EF

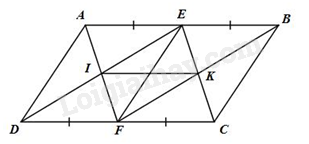
a) Ta có:
\(AE = EB = \frac{1}{2}AB\) (do \(E\) là trung điểm của \(AB\))
\(DF = FC = \frac{1}{2}CD\) (\(F\) là trung điểm của \(CD\))
\(AB = CD\) (do \(ABCD\) là hình bình hành)
Suy ra \(AE = CF = EB = DF\)
Xét tứ giác \(AECF\) ta có:
\(AE\) // \(CF\) (do \(AB\) // \(CD\))
\(AE = CF\)
Suy ra \(AECF\) là hình bình hành
b) Vì \(AB = 2AD\) (gt) và \(AB = 2AE\) (do \(E\) là trung điểm của \(AB\))
Suy ra \(AD = AE\)
Xét tứ giác \(AEFD\) có \(AE\) // \(DF\) và \(AE = DF\) (cmt)
Suy ra \(AEFD\) là hình bình hành
Mà \(AE = AD\) (cmt)
Suy ra \(AEFD\) là hình thoi
c) Ta có \(AF \bot DE\) (do \(AEFD\) là hình thoi)
và \(AF\) // \(EC\) (\(AECF\) là hình bình hành)
Suy ra \(EC \bot DE\)
Suy ra \(\widehat {IEK} = 90^\circ \)
Vì \(AEFD\) là hình thoi nên \(EF = AE\)
Và \(AE = \frac{1}{2}AB\) (gt)
Suy ra \(EF = \frac{1}{2}AB\)
Xét \(\Delta AFB\) có \(FE\) là đường trung tuyến và \(EF = \frac{1}{2}AB\)
Suy ra \(\Delta AFB\) vuông tại \(F\)
Suy ra \(\widehat {{\rm{IFK}}} = 90\)
Xét tứ giác \(EIFK\) ta có:
\(\widehat {{\rm{EIF}}} = 90\) (do \(AF \bot DE\))
\(\widehat {{\rm{IEK}}} = 90^\circ \) (cmt)
\(\widehat {{\rm{IFK}}} = 90^\circ \) (cmt)
Suy ra \(EIFK\) là hình chữ nhật
d) \(EIFK\) là hình vuông
Suy ra \(FI = EI\)
Mà \(EI = ID = \frac{1}{2}DE\) ( do \(AEFD\) là hình thoi)
\(FI = IA = \frac{1}{2}AF\) (do \(AEFD\) là hình thoi)
Suy ra \(AF = DE\)
Mà \(AEFD\) là hình thoi
Suy ra \(AEFD\) là hình chữ nhật
Suy ra \(\widehat {{\rm{ADC}}} = 90^\circ \)
Mà \(ABCD\) là hình bình hành (gt)
Suy ra \(ABCD\) là hình chữ nhật
Vậy nếu hình bình hành \(ABCD\) là hình chữ nhật thì \(EIFK\) là hình vuông