Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

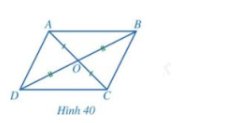
a) Vì ABCD là hình bình hành nên AB // CD; AD // BC.
Suy ra \(\widehat {BAC} = \widehat {AC{\rm{D}}};\widehat {BCA} = \widehat {DAC}\)(hai góc so le trong).
Xét ∆ABC và ∆CDA có:
\(\widehat {BAC} = \widehat {AC{\rm{D}}}\) (chứng minh trên);
Cạnh AC chung.
\(\widehat {BCA} = \widehat {DAC}\) (chứng minh trên);
Do đó ∆ABC = ∆CDA (g.c.g).
Suy ra AB = CD, AD = BC (các cặp cạnh tương ứng); \(\widehat {ABC} = \widehat {C{\rm{D}}A}\) (hai góc tương ứng).
b) Xét ∆ABD và ∆CDB có:
AB = CD (chứng minh trên);
AD = BC (chứng minh trên);
Cạnh BD chung.
Do đó ∆ABD = ∆CDB.
Suy ra \(\widehat {DAB} = \widehat {BC{\rm{D}}}\) (hai góc tương ứng).
c) Xét ∆AOB và ∆COD có:
\(\widehat {BAC} = \widehat {AC{\rm{D}}}\) (chứng minh trên);
AB = CD (chứng minh trên);
\(\widehat {BCA} = \widehat {DAC}\) (chứng minh trên);
Do đó ∆AOB = ∆COD (g.c.g).
Suy ra OA = OC, OB = OD (các cặp cạnh tương ứng).

a, Xét \(\Delta ADC\)và \(\Delta BDC\)có:
DC là cạnh chung.
\(\widehat {ADC} = \widehat {BCD}\)(do ABCD là hình thang cân)
AD = BC
\( \Rightarrow \Delta ADC = \Delta BDC(c.g.c)\)
\( \Rightarrow \widehat {CAD} = \widehat {DBC}\)(2 góc tương ứng) hay
Do: \(\Delta ADC = \Delta BDC\)
Xét \(\Delta BAD\)và \(\Delta ACB\)có:
AB chung
AD = BC
AC = BD
\( \Rightarrow \Delta BDA = \Delta ACB\) (c.c.c)
\( \Rightarrow \widehat {BDA} = \widehat {ACB}\)(2 góc tương ứng) hay \(\widehat {TDA} = \widehat {TCB}\)
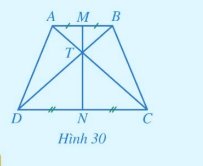
b, Xét \(\Delta TAD\)và \(\Delta TBC\)có:
\(\widehat {TAD} = \widehat {TBC}\)(theo câu a)
AD = BC (ABCD là hình thang cân)
\(\widehat {TDA} = \widehat {TCB}\)(theo câu a)
\( \Rightarrow \Delta TAD = \Delta TBC \Rightarrow TA = TB,TC = TD\)
c, Vì: TA = TB \( \Rightarrow \Delta ATB\)cân tại T suy ra TM là trung trực của AB
TC = TD \( \Rightarrow \Delta DTC\)cân tại T suy ra TN là trung trực của CD
Mà: M, T, N thẳng hàng. Nên MN là đường trung trực của cả 2 đường thẳng AB và CD

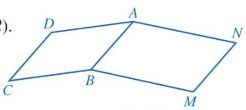
a, Do ABCD là hình bình hành: AB = CD.
Do ABMN là hình bình hành: AB = MN
Suy ra: CD = MN = AB
b, Do ABCD là hình bình hành \( \Rightarrow \widehat {BCD} = \widehat {DAB}\)
Do ABMN là hình bình hành \( \Rightarrow \widehat {BMN} = \widehat {NAB}\)
\(\widehat {BCD} + \widehat {BMN} = \widehat {DAB} + \widehat {NAB} = \widehat {DAN}\)

a) Xét hai tam giác ABC và CDA có:AB = CD; AD = BC; AC chung nên \(\Delta ABC = \Delta C{\rm{D}}A(c - c - c)\)
Suy ra: \(\widehat {BAC}\) = \(\widehat {DCA};\widehat {ACB}\) = \(\widehat {CAD}\).
Nên ABCD hình bình hành.
b) Xét hai tam giác ABO và tam giác CDO có: \(OA = OB;\widehat {AOB} = \widehat {CO{\rm{D}}};OC = O{\rm{D}}\)
Suy ra: \(\Delta ABO = \Delta C{\rm{D}}O\)
Suy ra: \(\widehat {BAC}\) = \(\widehat {DCA};\widehat {ACB}\) = \(\widehat {CA{\rm{D}}}\).
Nên ABCD là hình bình hành.

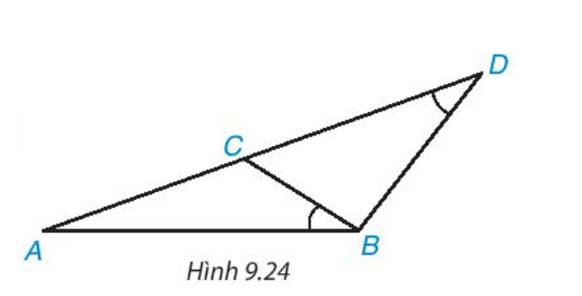
Xét tam giác ABC và tam giác ADB có
\(\widehat {ABC} = \widehat {A{\rm{D}}B}\) và \(\widehat A\) chung
=> ΔABC ∽ ΔADB (g.g)
=> \(\frac{{AB}}{{AD}} = \frac{{AC}}{{AB}}\)
=> \(A{B^2} = A{\rm{D}}.AC\)

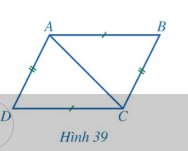
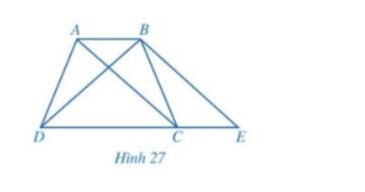
Do ABCD là hình thang nên AB//CD.
Kẻ BE//AC, \(E \in CD\) nên CE//AB.
\( \Rightarrow \widehat {BCE} = \widehat {ABC}\); \(\widehat {CBE} = \widehat {ACB}\) (hai góc so le trong).
a, Xét \(\Delta ABC\)và \(\Delta ECB\) có:
\(\widehat {BCE} = \widehat {ABC}\)
BC chung
\(\widehat {CBE} = \widehat {ACB}\) (do BC//AC )
\( \Rightarrow \Delta ABC = \Delta ECB\)(g.c.g)
b, BE = AC = BD
\( \Rightarrow \Delta BDE\)cân tại B
\( \Rightarrow \widehat {BDE} = \widehat {BED}\)
Do \(\Delta ABC = \Delta ECB\)
\( \Rightarrow \widehat {BEC} = \widehat {BAC}\) (2 góc tương ứng) hay \(\widehat {BED} = \widehat {BAC}(1)\)
Mà: \(\widehat {BAC} = \widehat {ACD}\) (do AB//CD) (2)
Từ (1), (2) suy ra: \(\widehat {BED} = \widehat {ACD}\)
c, Theo câu b:
\(\begin{array}{l}\widehat {BED} = \widehat {BDE}\\\widehat {ACD} = \widehat {BED}\end{array}\) suy ra: \(\widehat {ACD} = \widehat {BDE}\) hay \(\widehat {ACD} = \widehat {BDC}\)
Xét \(\Delta ACD\)và \(\Delta BDC\)có:
CD chung
\(\widehat {ACD} = \widehat {BDC}\)
AC = BD (gt)
\( \Rightarrow \Delta ACD = \Delta BDC(c.g.c)\)
\( \Rightarrow \widehat {ADC} = \widehat {BCD}\) (2 góc tương ứng)
d, Hình thang ABCD (AB//CD) có \(\widehat {ADC} = \widehat {BCD}\)nên hình thang ABCD là hình thang cân.

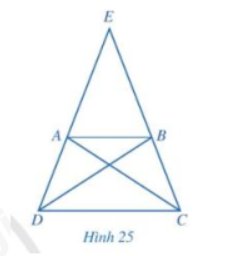
a, Do ABCD là hình thang cân nên.
\(\widehat {ADC} = \widehat {BCD}\)hay \(\widehat {EDC} = \widehat {ECD}\)
Do ABCD là hình thang cân nên
\(\widehat {BAD} = \widehat {ABC}\left( 1 \right)\)
Mà:
\(\begin{array}{l}\widehat {BAD} + \widehat {EAB} = {180^0}\\\widehat {ABC} + \widehat {EBA} = {180^0}\end{array}\)
Suy ra:
\(\begin{array}{l}\widehat {BAD} + \widehat {EAB} = \widehat {ABC} + \widehat {EBC}\\ \Rightarrow \widehat {EAB} = \widehat {EBA}\end{array}\)(do(1))
b, Do \(\widehat {EAB} = \widehat {EBA}\) suy ra \(\Delta EAB\)cân tại E nên EA = EB
Do \(\widehat {EDC} = \widehat {ECD}\) suy ra \(\Delta ECD\)cân tại E nên ED = EC
Mà: ED = EC
Suy ra EA + AD = EB + BC
Suy ra AD = BC (do EA = EB)
c, Xét \(\Delta ADC\) và \(\Delta BCD\) có:
AD = BC
\(\widehat {ADC} = \widehat {BCD}\)
DC chung
Suy ra: \(\Delta ADC = \Delta BCD(c.g.c) \Rightarrow AC = BD\)

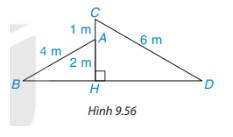
Xét hai tam giác vuông HBA và tam giác vuông HDC nhận thấy:
\(\frac{{AB}}{{C{\rm{D}}}} = \frac{{AH}}{{CH}} = \frac{2}{3}\)
=> Hai tam giác đồng dạng
\( \Rightarrow \widehat {AB{\rm{D}}} = \widehat {C{\rm{D}}B}\)

a)
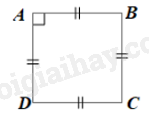
\(ABCD\) là hình thoi nên cũng là hình bình hành.
Suy ra:
\(AB = BC = CD = DA\);
\(\widehat A = \widehat C;\;\widehat B = \widehat D\)
\(\widehat A + \widehat B + \widehat C + \widehat D = 360^\circ \)
Suy ra: \(\widehat A + \widehat B = \widehat C + \widehat D = 180^\circ \)
Mà \(\widehat {BAD}\) là góc vuông
Suy ra \(\widehat {BCD} = 90^\circ \); \(\widehat B = 90^\circ ;\;\widehat D = 90^\circ \)
b) Nếu \(AC = BD\) thì \(ABCD\) là hình chữ nhật
Khi đó \(\widehat {BAD}\) là góc vuông


a) Vì \(ABCD\) là hình bình hành (gt)
Suy ra \(O\) là trung điểm của \(AC\), \(BD\)
\(AB = CD\); \(AD = BC\); \(AB\) // \(CD\); \(AD\) // \(BC\)
Nếu \(\widehat {{\rm{BAD}}} = 90^\circ \) suy ra \(AB \bot AD\)
Mà \(AB\) // \(CD\); \(AD\) // \(BC\)
Suy ra \(AD \bot CD;\;AB \bot BC\)
Suy ra \(\widehat {ADC} = \widehat {ABC} = 90^\circ \)
b) Xét \(\Delta BAD\) và \(\Delta CDA\) ta có:
\(BA = CD\) (gt)
\(AD\) chung
\(BD = AC\) (gt)
Suy ra \(\Delta BAD = \Delta CDA\) (c-c-c)
Suy ra \(\widehat {{\rm{BAD}}} = \widehat {{\rm{CDA}}}\) (hai góc tương ứng)
Mà \(\widehat {BAD} + \widehat {CDA} = 180^\circ \)(do \(AB\) // \(CD\) , cặp góc trong cùng phía)
Suy ra \(\widehat {BAD} = \widehat {CDA} = 90^\circ \)