Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔAED vuông tại E và ΔCFB vuông tại F có
AD=CB
\(\widehat{ADE}=\widehat{CBF}\)
Do đó: ΔAED=ΔCFB
Suy ra AE=CF: ED=FB
Xét tứ giác AECF có
AE//CF
AE=CF
Do đó: AECF là hình bình hành
b: Xét ΔKBF vuông tại F và ΔIDE vuông tại E có
FB=ED
\(\widehat{KBF}=\widehat{IDE}\)
Do đó: ΔKBF=ΔIDE
Suy ra: KB=ID
Xét tứ giác KBID có
KB//ID
KB=ID
Do đó: KBID là hình bình hành
Suy ra: Hai đường chéo KI và BD cắt nhau tại trung điểm của mỗi đường

a: Xét ΔAED vuông tại E và ΔCFB vuông tại F có
AD=CB
\(\widehat{ADE}=\widehat{CBF}\)
Do đó: ΔAED=ΔCFB
Suy ra: AE=CF và DE=BF
Xét tứ giác AECF có
AE//CF
AE=CF
Do đó: AECF là hình bình hành
b: Xét ΔKBF vuông tại F và ΔIDE vuông tại E có
KB=ID
\(\widehat{KBF}=\widehat{IDE}\)
Do đó: ΔKBF=ΔIDE
Suy ra: KB=ID
Xét tứ giác BKDI có
BK//ID
BK=ID
Do đó: BKDI là hình bình hành
Suy ra: Hai đường chéo BD và KI cắt nhau tại trung điểm của mỗi đường

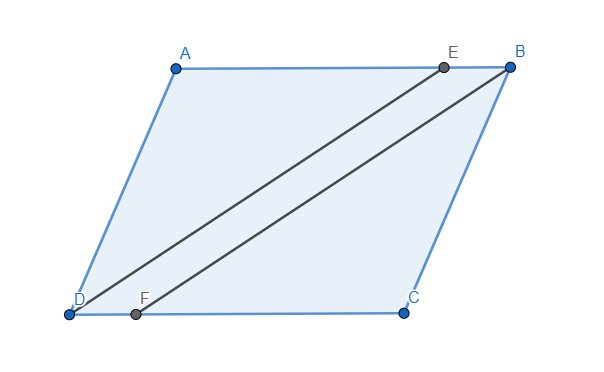
a) Ta thấy \(\widehat{AED}=\widehat{EDC}=\widehat{ADE}\) nên tam giác ADE cân tại A. Hoàn toàn tương tự thì tam giác CBF cân tại C.
Mặt khác, do tứ giác ABCD là hình bình hành nên \(\widehat{A}=\widehat{C},\widehat{B}=\widehat{D}\). Do đó \(\dfrac{\widehat{B}}{2}=\dfrac{\widehat{D}}{2}\) hay \(\widehat{CBF}=\widehat{ADE}\). Kết hợp với \(\widehat{A}=\widehat{C}\) thì suy ra \(\Delta ADE~\Delta CBF\left(g.g\right)\). Lại có \(\dfrac{AD}{CB}=1\) (do tứ giác ABCD là hình bình hành), suy ra \(\Delta ADE=\Delta CBF\) (2 tam giác đồng dạng có tỉ số đồng dạng bằng 1 thì 2 tam giác đó bằng nhau), ta có đpcm.
b) Ta thấy \(\widehat{AED}=\widehat{ADE}=\widehat{CBF}=\widehat{ABF}\) nên DE//BF. Lại có BE//DF (do tứ giác ABCD là hình bình hành) nên tứ giác DEBF cũng là hình bình hành (các cặp cạnh đối song song).
A B C D E F
a/
Xét tg ADE có
\(\widehat{ADE}=\widehat{CDE}\) (gt) (1)
\(\widehat{AED}=\widehat{CDE}\) (góc so le trong) (1)
Từ (1) và (2) => \(\widehat{ADE}=\widehat{AED}\) => tg ADE là tg cân tại A
=> AD=AE (3)
Xét tg CBF có
\(\widehat{CBF}=\widehat{ABF}\) (gt) (4)
\(\widehat{CFB}=\widehat{ABF}\) (góc so le trong) (5)
Từ (4) và (5) => \(\widehat{CBF}=\widehat{CFB}\) => tg CBF cân tại C
=> CB=CF (6)
Ta có
AD=CB (cạnh đối hình bình hành) (7)
Từ (3) (6) (7) => AD=AE=CB=CF
Mà \(\widehat{DAE}=\widehat{BCF}\) (góc đối hình bình hành)
=> tg ADE = tg CBF (c.g.c)
=> tg ADE và tg CBF là những tg cân bằng nhau
b/
tg ADE = tg CBF (cmt) \(\Rightarrow\widehat{BFC}=\widehat{ADE}\)
Mà \(\widehat{EDC}=\widehat{ADE}\) (gt)
\(\Rightarrow\widehat{BFC}=\widehat{EDC}\) Hai góc này ở vị trí đồng vị => DE//BF (8)
Ta có
AB//CD (cạnh đối hình bình hành) => BE//DF (9)
Từ (8) (9) => DEBF là hình bình hành (tứ giác có các cặp cạnh đối // với nhau là hình bình hành)

a) Ta có :
\(\hept{\begin{cases}NE\perp DM\\MG\perp BN\end{cases}}\)
\(\Rightarrow DM//BN\)
\(\Rightarrow\widehat{EDN}=\widehat{GBM}\)( sole trong) (1)
Mà \(\widehat{ADE}=\widehat{EDN}\)(2)
Từ (1) và(2)
\(\Rightarrow\widehat{ADE}=\widehat{GBM}\)
Lại có : \(DM//BN\left(cmt\right)\)
\(\Rightarrow\widehat{AMD}=\widehat{GBM}\)
\(\Rightarrow\widehat{ADM}=\widehat{AMD}\)
=> Tam giác ADM cân tại A
\(\Rightarrow AM=AD\left(dpcm\right)\)
b) P/s: phải là chứng minh tam giác MGB và tam giác NED chớ không phải tam giác MHB bạn ơi .
giải : Xét \(\Delta MGB\)và \(\Delta NED\)ta có :
\(MB=DN\)
\(\widehat{E}=\widehat{G}=90^o\)
\(\widehat{EDN}=\widehat{GBM}\)( câu a )
=> \(\Delta MGB=\Delta NED\)( cạnh huyền - góc nhọn )
c) Vì ABCD là hình bình hành
\(\Rightarrow BM//DN\)( vì AB // CD ) (1)
Lại có : \(DM//BN\)( câu a ) (2)
Từ (1)và(2)
=> MBND là hình bình hành (đpcm)