Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Hoành độ các giao điểm của đường thẳng d : y = x + 4 và độ thị hàm số y = x 3 + 2 m x 2 + ( m + 3 ) x + 4
là nghiệm của PT x 3 + 2 m x 2 + ( m + 3 ) x + 4 = x + 4 ⇒ x [ x 2 + 2 m x + ( m + 2 ) ] = 0
Điều kiện để tồn tại ba giao điểm là ∆ ' = m 2 - m - 2 = ( m + 1 ) ( m - 2 ) > 0 m + 2 ≢ 0 ⇔ m > 2 m < - 1 ( 1 ) m ≢ - 2
Khi đó tọa độ ba giao điểm là A(0;4) , B( A ( 0 ; 4 ) , B ( x 1 ; 4 + x 1 ) ) và C ( x 2 ; 4 + x 2 ) ⇒ B C → = ( x 2 - x 1 ; x 2 - x 1 )
Ta có B C = 2 ( x 2 - x 1 ) 2 = 2 x 2 + x 1 2 - 4 x 1 x 2 = 2 2 ( m 2 - m - 2 )
PT của đt BC là x - y + 4 = 0 ⇒ d M / B C = 1 - 3 + 4 1 2 + 1 2 = 2
Vậy nên S M B C = 1 2 2 . 2 2 ( m 2 - m - 2 ) = 2 ( m 2 - m - 2 ) = 4 ⇔ m 2 - m - 6 = 0 ⇒ m = - 2 m = 3
Kết hợp với điều kiện (1) ⇒ m = 3

Đáp án C.
Phương trình có hoành độ giao điểm của d và (C):
x 3 + 2 m x 2 + ( m + 3 ) x + 4 = x + 4 ⇔ x 2 + 2 m x + ( m + 2 ) = 0
Để d cắt (C) tại 3 điểm phân biệt A(0;4) và C thì phương trình (*) phải có hai nghiệm phân biệt x 1 , x 2 khác 0
⇔ 0 2 + 2 m . 0 + m + 2 ≢ 0 ∆ ' = m 2 - m - 2 > 0 ⇔ m + 2 ≢ 0 ( m + 1 ) ( m - 2 ) > 0 ⇔ m ≢ - 2 m > 2 m < - 1 ⇔ m > 2 m < - 1 m ≢ - 2 (1)
Giả sử B x 1 ; x 1 + 4 và B x 2 ; x 2 + 4 với x 1 , x 2 là hai nghiệm của (*)
Suy ra B C = 2 x 1 - x 2 và theo định lí Vi-ét: x 1 + x 2 = - 2 m x 1 x 2 = m + 2
Ta có S ∆ M B C = 1 2 d ( M ; B C ) . B C = 1 2 . 1 - 3 + 4 2 . 2 x 1 - x 2 = x 1 - x 2
Từ giả thiết ta có S ∆ M B C = 4 ⇔ x 1 - x 2 = 4 ⇔ x 1 - x 2 2 = 16
⇔ x 1 + x 2 2 - 4 x 1 x 2 = 16 ⇔ ( - 2 m ) 2 - 4 ( m + 2 ) - 16 = 0 ⇔ 4 m 2 - 4 m - 24 = 0
m = - 2 m = 3 . Đối chiếu với điều kiện (1), chỉ có m = 3 là thỏa mãn

Đáp án A.
Phương trình hoành độ giao điểm của c m và d : x 3 - 3 x 2 + ( m + 1 ) x + 1 = x + 1
⇔ x 3 - 3 x 2 + m x = 0 ⇔ x = 0 x 2 - 3 x + m = 0 *
Để c m cắt d tại ba điểm phân biệt P ( 0 ; 1 ) , M , N thì phương trình (*) phải có hai nghiệm phân biệt x 1 , x 2 khác 0 ⇔ 0 2 - 3 . 0 + m ≢ 0 ∆ = ( - 3 ) 2 - 4 m > 0 ⇔ m ≢ 0 m < 9 4
Giả sử M ( x 1 ; x 1 + 1 ) vàvới N ( x 2 ; x 2 + 1 ) là nghiệm của phương trình (*).
Theo định lý Vi-ét ta có x 1 + x 2 = 3 x 1 x 2 = m
Để tam giác OMN vuông tại O thì O M → . O N → = 0 ⇔ x 1 x 2 + ( x 1 + 1 ) ( x 2 + 1 ) = 0
⇔ 2 x 1 x 2 + ( x 1 + x 2 ) + 1 = 0 ⇔ 2 m + 4 = 0 ⇔ m = - 2 (thỏa mãn)

Đáp án D
Phương trình hoành độ giao điểm của )C) và(d) là
x + 2 x = x + m ⇔ x ≠ 0 x 2 + m − 1 x − 2 = 0 *
Để (C) cắt (d) tại 2 điểm phân biệt ⇔ * có 2 nghiệm phân biệt khác 0 ⇔ m ∈ ℝ
Khi đó, gọi A x 1 ; x 1 + 1 ; B x 2 ; x 2 + m ⇒ x 1 + x 2 = 1 − m là tọa độ giao điểm của (C) và(d)
Ta có: A B → = x 2 − x 1 ; x 2 − x 1 ⇒ u A B → = 1 ; 1 ; trung điểm AB là: I 1 − m 2 ; 1 + m 2
m = 0 ⇒ M , A , B thẳng hang (loại m = 0 )
Phương trình trung trực là: x + y − 1 = 0
Do M ∈ d ⇒ Δ M A D luôn cân tại M
Kết hợp với m ∈ ℤ và có 2018 giá trị m cần tìm

Đáp án C
Xét pt tương giao:
2 x - 1 x - 1 = x + m ⇔ 2 x - 1 - x + m x - 1 = 0 ⇔ x 2 - 3 - m x + m - 1 = 0
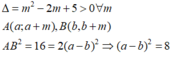
a + b 2 - 4 a b = 8 ⇔ 3 - m 2 - 4 1 - m = 8 ⇔ [ m = - 1 m = 3



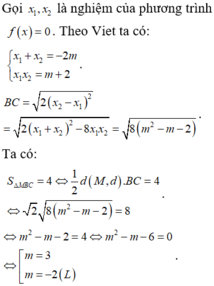

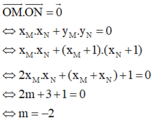

Đáp án A
Phương trình hoành độ giao điểm:
x 3 + 2 m x 2 + 3 ( m − 1 ) x+ 2 = − x+ 2 ⇔ x 3 + 2 m x 2 + ( 3 m − 2 ) x= 0 ⇔ x= 0 x 2 + 2 m x + ( 3 m − 2 ) = 0
+) Với m= -1 ba giao điểm là A 0 ; 2 , B 1 − 6 ; 1 + 6 , C 1 + 6 ; 1 − 6
MB = 16 + 4 6 ; MC = 16 − 4 6 ; BC = 4 3
Diện tích tam giác MBC=2 6
+) Với m= 4 ba giao điểm là A 0 ; 2 , B − 4 + 6 ; − 2 + 6 , C − 4 − 6 ; − 2 − 6
MB = 70 − 20 6 ; MC = 70 + 20 6 ; BC = 4 3
Diện tích tam giác MBC ≈ 9,1
Vậy m=-1