Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1:
\(A=x^2y-y+xy^2-x=\left(x^2y+xy^2\right)-\left(x+y\right)\\ =xy\left(x+y\right)-\left(x+y\right)=\left(x+y\right)\left(xy-1\right)\)
Voqis x=-1;y=3 ta có:
\(A=\left(-1+3\right)\left(-1\cdot3-1\right)=2\cdot\left(-4\right)=-8\)
b) \(B=x^2y^2+xy+x^3+y^3=\left(x^2y^2+x^3\right)+\left(xy+y^3\right)\\ =x^2\left(y^2+x\right)+y\left(x+y^2\right)=\left(x+y^2\right)\left(x^2+y\right)\)
Với x=-1;y=3 ta có:
\(B=\left(-1+3^2\right)\left(-1^2+3\right)=8\cdot2=16\)
c) \(C=2x+xy^2-x^2y-2y=\left(2x-2y\right)+\left(xy^2-x^2y\right)\\ =2\left(x-y\right)+xy\left(y-x\right)=\left(x-y\right)\left(2-xy\right)\)
Với x=-1;y=3 ta có:
\(C=\left(-1-3\right)\left(2-\left(-1\right)\cdot3\right)=-4\cdot5=-20\)
d) phân tích tt

\(a,\)Có :\(f\left(0\right)=3.0+1=1\)
\(f\left(-1\right)=-1.3-1=-3-1=-4\)
\(f\left(-\frac{1}{3}\right)=3.\left(-\frac{1}{3}\right)-1=-1-1=-2\)
\(b,\)Có \(3x-1=-16\)
\(\Rightarrow3x=-15\)
\(\Rightarrow x=-5\)
Vậy x = - 5 để y = -16
GIẢI:
a) f(0)=-1
f(-1)=-4
f(-1/3)=-2
b) 3x-1=-16
3x=-16+1
3x=-15
x=-15:3
x=-5.
vậy x=-5

Câu 5:
a: Khi m=3 thì \(f\left(x\right)=\left(2\cdot3+1\right)x-3=7x-3\)
\(f\left(-3\right)=7\cdot\left(-3\right)-3=-21-3=-24\)
\(f\left(0\right)=7\cdot0-3=-3\)
b: Thay x=2 và y=3 vào f(x)=(2m+1)x-3, ta được:
\(2\left(2m+1\right)-3=3\)
=>2(2m+1)=6
=>2m+1=3
=>2m=2
=>m=1
c: Thay m=1 vào hàm số, ta được:
\(y=\left(2\cdot1+1\right)x-3=3x-3\)
*Vẽ đồ thị
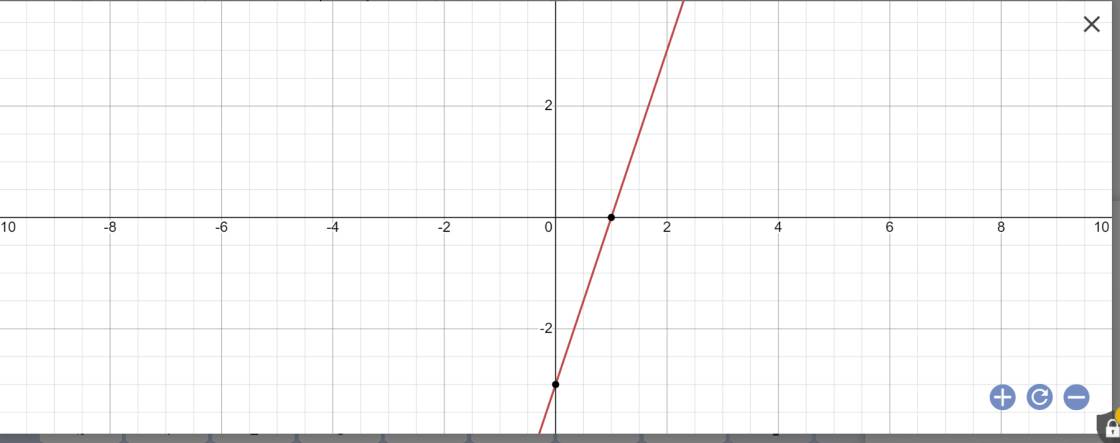
d: Để hàm số y=(2m+1)x-3 là hàm số bậc nhất thì \(2m+1\ne0\)
=>\(2m\ne-1\)
=>\(m\ne-\dfrac{1}{2}\)
e: Để đồ thị hàm số y=(2m+1)x-3 song song với đường thẳng y=5x+1 thì \(\left\{{}\begin{matrix}2m+1=5\\-3\ne1\end{matrix}\right.\)
=>2m+1=5
=>2m=4
=>m=2

c) thay x=1 vào đa thức f(x) ta có: f(1)=4.1^3-1^2+2.1-5
=4-2+2-5
=- 1
vậy 1 k phải là nghiệm của đa thức f(x)
MÌNH CHỈ LÀM ĐƯỢC C THÔI HOK TỐT
làm sai nha chỗ nào là 1 thì thay bằng -1 nha kq sẽ ra nha

a) Đặt tính đa thức chia đa thức ta được:
\(f\left(x\right):g\left(x\right)=\left(x^2+x\right)\).
b) Thương f(x) : g(x) =0
<=> \(x^2+x=0\)
<=> x ( x + 1 ) = 0
<=> x =0 hoặc x+1 =0
<=> x=0 hoặc x=-1.
c)
Ta có: \(f\left(x\right):g\left(x\right)=\left(x^2+x\right)=x^2+2.x.\frac{1}{2}+\frac{1}{4}-\frac{1}{4}=\left(x+\frac{1}{2}\right)^2-\frac{1}{4}\ge-\frac{1}{4}\).
Gía trị nhỏ nhất là -1/4 đạt tại x = -1/2.
( Cảm ơn em đã giúp đỡ các bạn khác :)

\(f\left(x\right).g\left(x\right)+x^2.[1-3.g\left(x\right)]=\frac{5}{2}\)
\(\Rightarrow f\left(x\right).g\left(x\right)+x^2-3x^2.g\left(x\right)=\frac{5}{2}\) (1)
Ta thay: \(f\left(x\right)=3x^2-x+1\) và \(g\left(x\right)=x-1\) vào (1) ta được
\(\left(3x^2-x+1\right).\left(x-1\right)+x^2-3x^2.\left(x-1\right)=\frac{5}{2}\)
\(\Rightarrow\left(x-1\right).\left(3x^2-x+1-3x^2\right)+x^2=\frac{5}{2}\)
\(\Rightarrow\left(x-1\right).\left(-x+1\right)+x^2=\frac{5}{2}\)
\(\Rightarrow-\left(x-1\right)^2+x^2=\frac{5}{2}\)
\(\Rightarrow-x^2+2x-1+x^2=\frac{5}{2}\)
\(\Rightarrow2x=\frac{7}{2}\)
\(\Rightarrow x=\frac{7}{4}\)
a) \(f\left(x\right).g\left(x\right)=\left(3x^2-x+1\right).\left(x-1\right)\)
\(=x.\left(3x^2-x+1\right)-\left(3x^2-x+1\right)\)
\(=3x^3-x^2+x-3x^2+x-1\)
\(=3x^3-4x^2+2x-1\)
b) \(f\left(x\right).g\left(x\right)+x^2.\left[1-3.g\left(x\right)\right]=\frac{5}{2}\)
=> \(3x^3-4x^2+2x-1+x^2.\left(1-3x+3\right)=\frac{5}{2}\)
=> \(3x^3-4x^2+2x-1+x^2-3x^3+3x^2=\frac{5}{2}\)
=> \(2x-1=\frac{5}{2}\)
=>\(2x=\frac{5}{2}+1=\frac{5+2}{2}=\frac{7}{2}\)
=>\(x=\frac{7}{2}:2=\frac{7}{4}\)
a: \(F\left(3\right)=3\left(3-2\right)=3\cdot1=3\)
\(\left[F\left(\dfrac{2}{3}\right)\right]^2=\left[\dfrac{2}{3}\cdot\left(\dfrac{2}{3}-2\right)\right]^2\)
\(=\left[\dfrac{2}{3}\cdot\dfrac{-4}{3}\right]^2=\left(-\dfrac{8}{9}\right)^2=\dfrac{64}{81}\)
\(G\left(-\dfrac{1}{2}\right)=-\left(-\dfrac{1}{2}\right)+6=6+\dfrac{1}{2}=\dfrac{13}{2}\)
b: F(x)=0
=>x(x-2)=0
=>\(\left[{}\begin{matrix}x=0\\x-2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=2\end{matrix}\right.\)
c: F(a)=G(a)
=>\(a\left(a-2\right)=-a+6\)
=>\(a^2-2a+a-6=0\)
=>\(a^2-a-6=0\)
=>(a-3)(a+2)=0
=>\(\left[{}\begin{matrix}a-3=0\\a+2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}a=3\\a=-2\end{matrix}\right.\)