Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

b)
=>\(\left\{{}\begin{matrix}m-1>2\\m+3\le5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m>3\\m\le2\end{matrix}\right.\)(vô lý)
vậy ko tồn tại m

1; Cho 2 tập hợp A là tập hợp của 3;7 và B là tập hợp của 1;3;7 khi đó ta có
a/ A là tập con của B b/ A là tập chứa của B c/ A bằng B d/ A thuộc B
2; Viết tập hợp P các chữ của số 3456
a/ P bằng 2;6;3;5 b/ P bằng 3;5 c/ P bằng 3;4;5;6 đ/ P bằng 3456

Lời giải:
Biểu diễn tập A,B trên trục số bạn sẽ thấy để $A\cap B$ nhận 1 giá trị duy nhất khi:
\(\left[\begin{matrix} m^2+1=3m-1\\ -3=4(\text{vô lý})\end{matrix}\right.\Rightarrow m^2-3m+2=0\Leftrightarrow (m-1)(m-2)=0\)
\(\Rightarrow \left[\begin{matrix} m=1\\ m=2\end{matrix}\right.\)
Thử lại thấy $m=2$ không thỏa mãn vì khi đó $3m-1>4$
Vậy có 1 giá trị nguyên của $m$ thỏa mãn
Đáp án C
Lời giải:
Biểu diễn tập A,B trên trục số bạn sẽ thấy để $A\cap B$ nhận 1 giá trị duy nhất khi:
\(\left[\begin{matrix} m^2+1=3m-1\\ -3=4(\text{vô lý})\end{matrix}\right.\Rightarrow m^2-3m+2=0\Leftrightarrow (m-1)(m-2)=0\)
\(\Rightarrow \left[\begin{matrix} m=1\\ m=2\end{matrix}\right.\)
Thử lại thấy $m=2$ không thỏa mãn vì khi đó $3m-1>4$
Vậy có 1 giá trị nguyên của $m$ thỏa mãn
Đáp án C

a: \(y=-x^2+2x+3\)
y>0
=>\(-x^2+2x+3>0\)
=>\(x^2-2x-3< 0\)
=>(x-3)(x+1)<0
TH1: \(\left\{{}\begin{matrix}x-3>0\\x+1< 0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x>3\\x< -1\end{matrix}\right.\)
=>\(x\in\varnothing\)
TH2: \(\left\{{}\begin{matrix}x-3< 0\\x+1>0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x< 3\\x>-1\end{matrix}\right.\)
=>-1<x<3
\(y=\dfrac{1}{2}x^2+x+4\)
y>0
=>\(\dfrac{1}{2}x^2+x+4>0\)
\(\Leftrightarrow x^2+2x+8>0\)
=>\(x^2+2x+1+7>0\)
=>\(\left(x+1\right)^2+7>0\)(luôn đúng)
b: \(y=-x^2+2x+3< 0\)
=>\(x^2-2x-3>0\)
=>(x-3)(x+1)>0
TH1: \(\left\{{}\begin{matrix}x-3>0\\x+1>0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x>3\\x>-1\end{matrix}\right.\)
=>x>3
TH2: \(\left\{{}\begin{matrix}x-3< 0\\x+1< 0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x< 3\\x< -1\end{matrix}\right.\)
=>x<-1
\(y=\dfrac{1}{2}x^2+x+4\)
\(y< 0\)
=>\(\dfrac{1}{2}x^2+x+4< 0\)
=>\(x^2+2x+8< 0\)
=>(x+1)2+7<0(vô lý)

a: \(A\cap B=\left(-3;1\right)\)
\(A\cup B\)=[-5;4]
A\B=[1;4]
\(C_RA\)=R\A=(-∞;-3]\(\cap\)(4;+∞)
b: C={1;-1;5;-5}
\(B\cap C=\left\{-5;-1\right\}\)
Các tập con là ∅; {-5}; {-1}; {-5;-1}

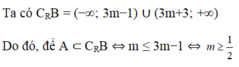
Từ biểu diễn của tập hợp B trên trục số, ta có điều kiện cần và đủ để A ⊂ B là
a ; a + 2 ⊂ ( − ∞ ; − 1 ) a ; a + 2 ⊂ ( 1 ; + ∞ ) ⇔ a + 2 < − 1 a > 1 ⇔ a < − 3 a > 1
Vậy tập hợp các giá trị của tham số a sao cho A ⊂ B là ( − ∞ ; − 3 ) ∪ ( 1 ; + ∞ )
Đáp án A