Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Hàm số \(y=2x+3k\) có các hệ số \(a=2,b=3k\)
Hàm số \(y=\left(2m+1\right)x+2k-3\) có các hệ số \(a'=2m+1,b'=2k-3\)
Hai hàm số đã cho là hàm số bậc nhất nên \(2m+1\ne0\)
\(\Leftrightarrow m\ne-\frac{1}{2}\)
Hai đường thẳng song song với nhau khi \(a=a'\) và \(b\ne b'\) tức là:
\(2=2m+1\) và \(3k\ne2k-3\)
Kết hợp với điều kiện trên ta có: \(m=\frac{1}{2}.k\ne-3\)
b) Hai đường thẳng song song:
\(\Leftrightarrow\hept{\begin{cases}2=2m+1\\3k\ne2k-3\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}m=\frac{1}{2}\\k\ne-3\end{cases}}\)
c) Hai đường thẳng trùng nhau:
\(\Leftrightarrow\hept{\begin{cases}2=2m+1\\3k=2k-3\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}m=\frac{1}{2}\\k=-3\end{cases}}\)

Hàm số y = mx + 3 có các hệ số a = m, b = 3.
Hàm số y = (2m + 1)x – 5 có các hệ số a' = 2m + 1, b' = -5
Vì hai hàm số là hai hàm số bậc nhất nên a và a' phải khác 0, tức là:
m ≠ 0 và 2m + 1 ≠ 0 hay
Theo đề bài ta có b ≠ b' (vì 3 ≠ -5)
Vậy đồ thị của hai hàm số là hai đường thẳng song song với nhau khi và chỉ khi a ≠ a' tức là:
m = 2m + 1 => m = - 1
Kết hợp với điều kiện trên ta thấy m = -1 là giá trị cần tìm.

Lời giải:
Hàm số bậc nhất nên điều kiện là:
\(m\neq 0; 2m+1\neq 0\Leftrightarrow m\neq 0; m\neq \frac{-1}{2}\)
1. Để 2 đường thẳng đã cho là 2 đường thẳng song song thì:
\(\left\{\begin{matrix} m=2m+1\\ 3\neq -5\end{matrix}\right.\Leftrightarrow m=-1\)
2. Để 2 đường thẳng đã cho cắt nhau thì:
\(m\neq 2m+1\Leftrightarrow m\neq -1\)
Kết hợp với điều kiên phía trên suy ra \(m\neq 0; m\neq -1; m\neq \frac{-1}{2}\)
Lời giải:
Hàm số bậc nhất nên điều kiện là:
\(m\neq 0; 2m+1\neq 0\Leftrightarrow m\neq 0; m\neq \frac{-1}{2}\)
1. Để 2 đường thẳng đã cho là 2 đường thẳng song song thì:
\(\left\{\begin{matrix} m=2m+1\\ 3\neq -5\end{matrix}\right.\Leftrightarrow m=-1\)
2. Để 2 đường thẳng đã cho cắt nhau thì:
\(m\neq 2m+1\Leftrightarrow m\neq -1\)
Kết hợp với điều kiên phía trên suy ra \(m\neq 0; m\neq -1; m\neq \frac{-1}{2}\)
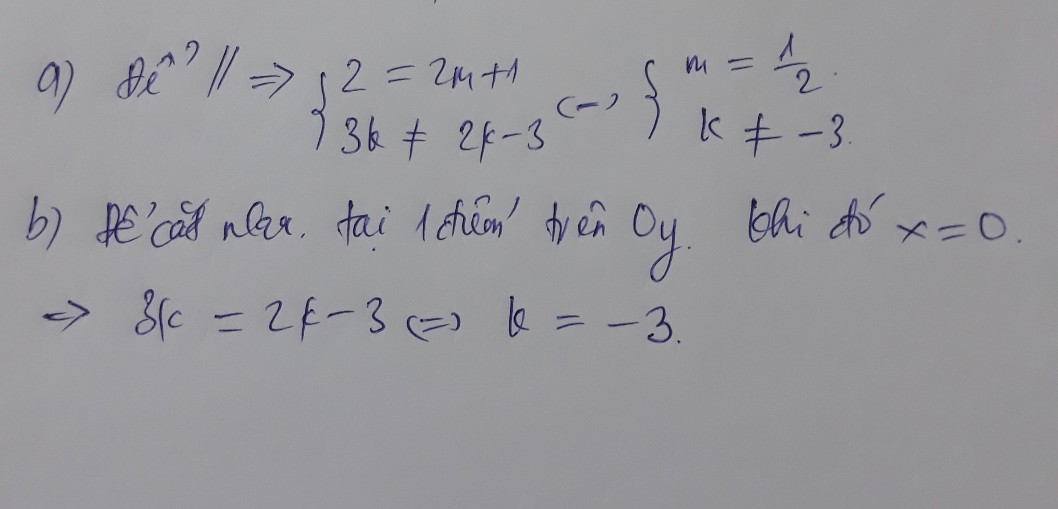
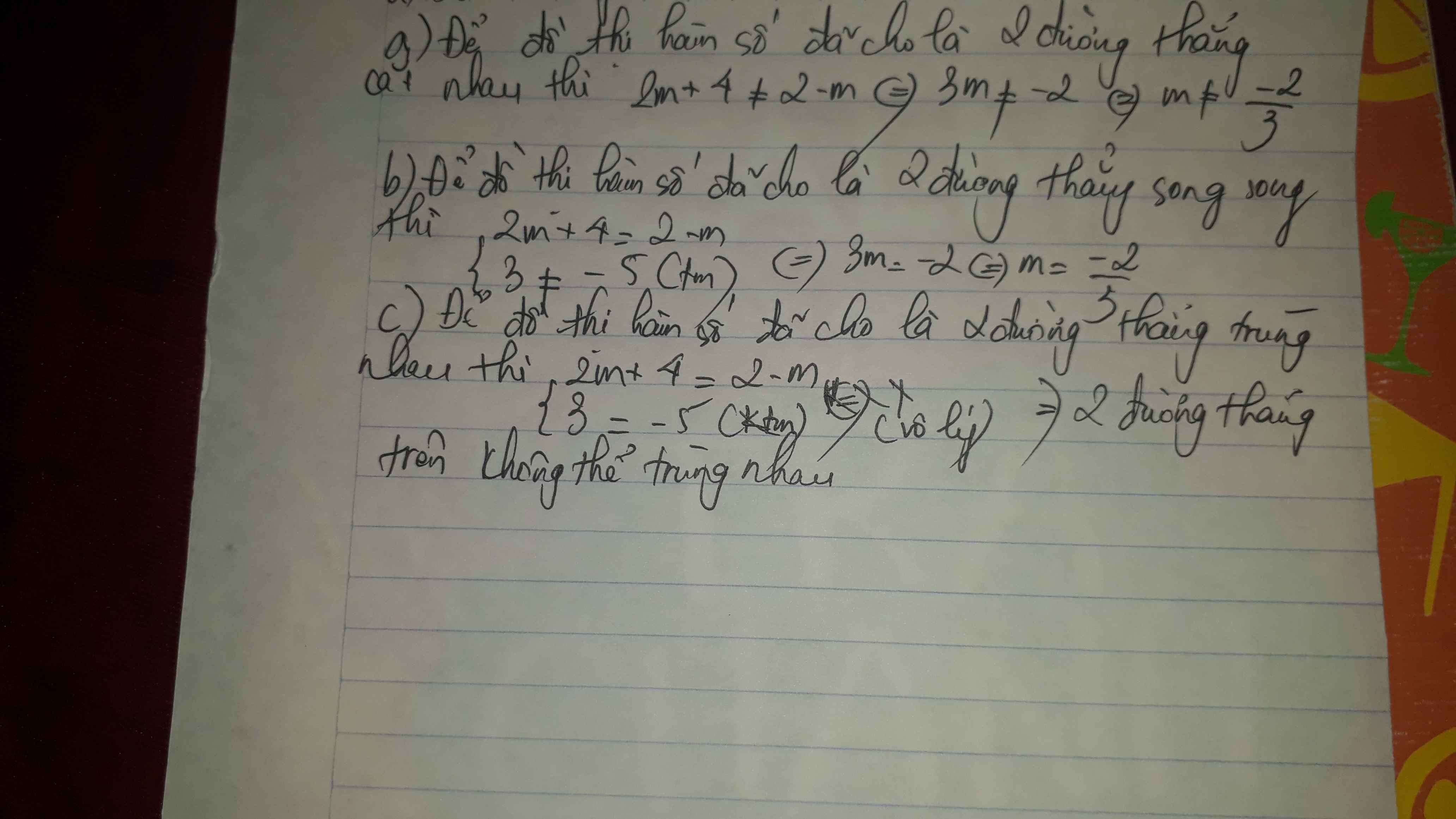
\(\left(1\right)\cap\left(2\right)\Leftrightarrow\left\{{}\begin{matrix}m+5\ne2m+1\\-2m+3\ne3m\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m\ne4\\m\ne\dfrac{3}{5}\end{matrix}\right.\\ \left(1\right)//\left(2\right)\Leftrightarrow\left\{{}\begin{matrix}m+5=2m+1\\-2m+3\ne3m\end{matrix}\right.\Leftrightarrow m=4\\ \left(1\right)\equiv\left(2\right)\Leftrightarrow\left\{{}\begin{matrix}m+5=2m+1\\-2m+3=3m\end{matrix}\right.\Leftrightarrow m\in\varnothing\)
a). Để hai hàm số cắt nhau thì:
a≠a'⇒ m+5=2m+1
⇔ m+5=2m+1
⇔ m-2m=1-5
⇔ -m = -4
⇔ m = 4.
Vậy hai hàm số cắt nhau khi m =4.
b). Để hai hàm số song song khi:
\(\left\{{}\begin{matrix}a=a'\\b\ne b'\end{matrix}\right.\)⇒\(\left\{{}\begin{matrix}m+5=2m+1\\-2m+3=3m\end{matrix}\right.\)⇔\(\left\{{}\begin{matrix}m=-4\\m\ne\dfrac{3}{5}\end{matrix}\right.\)
Vậy hai hàm số đó song song khi m=-4; m≠\(\dfrac{3}{5}\).
c). Để hai hàm số trùng nhau khi:
\(\left\{{}\begin{matrix}a=a'\\b=b'\end{matrix}\right.\)⇒\(\left\{{}\begin{matrix}m+5=2m+1\\-2m+3=3m\end{matrix}\right.\)⇔\(\left\{{}\begin{matrix}m=-4\\m=\dfrac{3}{5}\end{matrix}\right.\)
Vậy hai hàm số đó trùng nhau khi m=-4; m=\(\dfrac{3}{5}\).