Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: \(d\perp Ox;d\perp Oy\)
=>\(d\perp\left(Ox,Oy\right)\)
b: Số đo của \(\widehat{xOy}\) sẽ không đổi khi O di chuyển trên d
THAM KHẢO:
a) d⊥mp(Ox,Oy)
b) Khi O thay đổi trên d thì số đo góc \(\widehat{xOy}\)không đổi

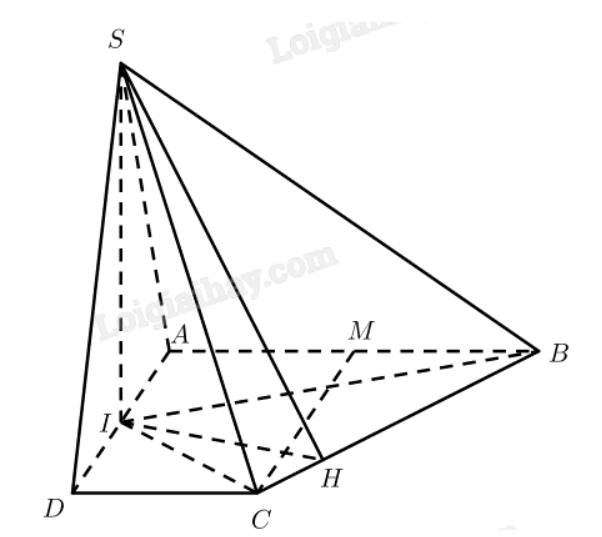
\(\left. \begin{array}{l}\left( {SBI} \right) \bot \left( {ABCD} \right)\\\left( {SCI} \right) \bot \left( {ABCD} \right)\\\left( {SBI} \right) \cap \left( {SCI} \right) = SI\end{array} \right\} \Rightarrow SI \bot \left( {ABCD} \right)\)
Kẻ \(IH \bot BC\left( {H \in BC} \right)\)
\(SI \bot \left( {ABCD} \right) \Rightarrow SI \bot BC\)
\( \Rightarrow BC \bot \left( {SIH} \right) \Rightarrow BC \bot SH\)
Vậy \(\widehat {AHI}\) là góc nhị diện \(\left[ {S,BC,A} \right]\)\( \Rightarrow \widehat {AHI} = {60^ \circ }\)
\(\begin{array}{l}{S_{ABC{\rm{D}}}} = \frac{1}{2}\left( {AB + C{\rm{D}}} \right).A{\rm{D}} = 3{a^2}\\AI = I{\rm{D}} = \frac{1}{2}A{\rm{D}} = a\\{S_{AIB}} = \frac{1}{2}AB.AI = {a^2},{S_{CI{\rm{D}}}} = \frac{1}{2}C{\rm{D}}.I{\rm{D}} = \frac{{{a^2}}}{2}\\ \Rightarrow {S_{BIC}} = {S_{ABC{\rm{D}}}} - {S_{AIB}} - {S_{CI{\rm{D}}}} = \frac{{3{a^2}}}{2}\end{array}\)
Gọi \(M\) là trung điểm của \(AB\)
\(\begin{array}{l} \Rightarrow BM = \frac{1}{2}AB = a,CM = AD = 2a \Rightarrow BC = \sqrt {B{M^2} + C{M^2}} = a\sqrt 5 \\ \Rightarrow IH = \frac{{2{{\rm{S}}_{BIC}}}}{{BC}} = \frac{{3a\sqrt 5 }}{5} \Rightarrow SI = IH.\tan \widehat {SHI} = \frac{{3a\sqrt {15} }}{5}\end{array}\)
\({V_{S.ABC{\rm{D}}}} = \frac{1}{3}{S_{ABC{\rm{D}}}}.SI = \frac{{3{a^3}\sqrt {15} }}{5}\)


a) Kẻ \(C'H \bot OC\left( {H \in OC} \right)\)
là hình chữ nhật \( \Rightarrow OH = O'C' = a,OO'\parallel C'H\)
Mà \(OO' \bot \left( {ABCDEF} \right)\)
\(\begin{array}{l} \Rightarrow C'H \bot \left( {ABCDEF} \right)\\ \Rightarrow \left( {CC',\left( {ABCDEF} \right)} \right) = \left( {CC',CH} \right) = \widehat {C'CH}\end{array}\)
\(\begin{array}{l}HC = OC - O'C' = \frac{a}{2},C'H = OO' = a\\ \Rightarrow \tan \widehat {C'CH} = \frac{{C'H}}{{HC}} = 2 \Rightarrow \widehat {C'CH} \approx 63,{4^ \circ }\end{array}\)
Vậy \(\left( {CC',\left( {ABCDEF} \right)} \right) \approx 63,{4^ \circ }\)
b) Gọi \(M,M'\) lần lượt là trung điểm của \(AB,A'B'\).
\( \Rightarrow OM \bot AB,O'M' \bot A'B'\)
\(ABB'A'\) là hình thang cân \( \Rightarrow MM' \bot AB,MM' \bot A'B'\)
\( \Rightarrow \left[ {O,AB,A'} \right] = \widehat {OMM'},\left[ {O',A'B',A} \right] = \widehat {O'M'M}\)
Kẻ \(M'K \bot OM\left( {K \in OM} \right)\)
\(OO'M'K\) là hình chữ nhật \( \Rightarrow OK = O'K' = \frac{{A'B'\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{4},OO' = M'K = a\)
\(\begin{array}{l}OM = \frac{{AB\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{2},MK = OM - OK = \frac{{a\sqrt 3 }}{4}\\ \Rightarrow \tan \widehat {OMM'} = \frac{{M'K}}{{MK}} = \frac{4}{{\sqrt 3 }} \Rightarrow \widehat {OMM'} \approx 66,{6^ \circ }\\ \Rightarrow \widehat {O'M'M} = {180^ \circ } - \widehat {OMM'} = 113,{4^ \circ }\end{array}\)

a) Góc giữa đường thẳng AB và mặt phẳng $(BCD)$ là góc giữa đường thẳng AB và một đường thẳng nằm trên mặt phẳng $(BCD)$ và // $BC$ hoặc $CD$. Vì ABCD là tứ diện đều, nên các cạnh của nó đều song song và bằng nhau.
=> AB//CD
Vậy góc giữa đường thẳng AB và mặt phẳng (BCD) là góc vuông.
b) Góc phẳng nhị diện [A,CD,B] là góc giữa mặt phẳng $(ACD)$ và mặt phẳng $(BCD)$. Vì $ABCD$ là tứ diện đều, nên mặt phẳng `(ACD)` ⊥ mặt phẳng $(BCD)$.
Do đó, góc phẳng nhị diện$ [A,CD,B] $là góc vuông.
Tương tự, góc phẳng nhị diện $[A,CD,E] $cũng là góc vuông.

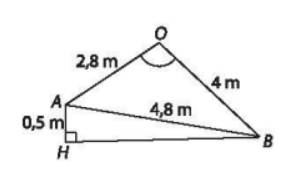
a) Vì hai mái nhà trong Hình 7.72 là hai hình chữ nhật nên góc nhị diện tạo bởi hai nửa mặt phẳng tương ứng chứa hai mái nhà là góc giữa hai đường thẳng OA và OB.
Xét tam giác OAB có
\(\cos \widehat {AOB} = \frac{{O{A^2} + O{B^2} - A{B^2}}}{{2OA.OB}} = \frac{{2,{8^2} + {4^2} - 4,{8^2}}}{{2.2,8.4}} = \frac{1}{{28}} \Rightarrow \widehat {AOB} \approx {88^0}\)
b) (OAB) vuông góc với đường nóc nhà, đường nóc nhà song song với mặt phẳng đất nên (OAB) vuông góc với mặt đất phẳng đất.
c) Đường thẳng qua B song song với mặt đất cắt đường thẳng qua A vuông góc với mặt đất tại H
Ta có \(\sin \widehat {ABH} = \frac{{0,5}}{{4,8}} \Rightarrow \widehat {ABH} \approx {6^0};\cos \widehat {OBA} = \frac{{13}}{{16}} \Rightarrow \widehat {OBA} \approx {36^0}\)
Do đó \(\widehat {OBH} = \widehat {ABH} + \widehat {OBA} \approx {42^0}.\)
Vậy góc giữa mái nhà (chứa OB) so với mặt đất khoảng 420

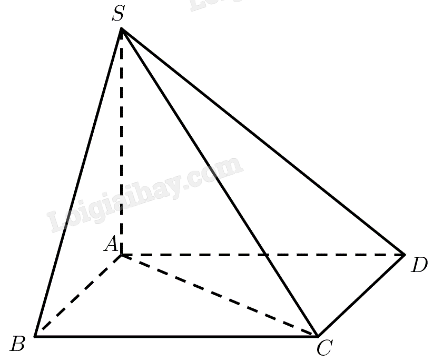
a) \(SA \bot \left( {ABCD} \right) \Rightarrow SA \bot AB,SA \bot A{\rm{C}}\)
Vậy \(\widehat {BA{\rm{C}}}\) là góc phẳng nhị diện của góc nhị diện \(\left[ {B,SA,C} \right]\)
\(AB = BC = AC = a \Rightarrow \Delta ABC\) đều \( \Rightarrow \widehat {BA{\rm{C}}} = \widehat {ABC} = {60^ \circ }\)
Vậy số đo của góc nhị diện \(\left[ {B,SA,C} \right]\) bằng \({60^ \circ }\).
b) \(SA \bot \left( {ABCD} \right) \Rightarrow SA \bot AB,SA \bot A{\rm{D}}\)
Vậy \(\widehat {BA{\rm{D}}}\) là góc phẳng nhị diện của góc nhị diện \(\left[ {B,SA,D} \right]\)
\(ABCD\) là hình thoi \( \Rightarrow \widehat {BA{\rm{D}}} = {180^ \circ } - \widehat {ABC} = {180^ \circ } - {60^ \circ } = {120^ \circ }\)
Vậy số đo của góc nhị diện \(\left[ {B,SA,D} \right]\) bằng \({120^ \circ }\).
c) \(SA \bot \left( {ABCD} \right) \Rightarrow \left( {SC,\left( {ABCD} \right)} \right) = \left( {SC,AC} \right) = \widehat {SCA}\)
\(\Delta SAC\) vuông tại \(A \Rightarrow \tan \widehat {SCA} = \frac{{SA}}{{AC}} = \frac{a}{a} = 1 \Rightarrow \widehat {SCA} = {45^ \circ }\)
Vậy \(\left( {SC,\left( {ABCD} \right)} \right) = {45^ \circ }\).
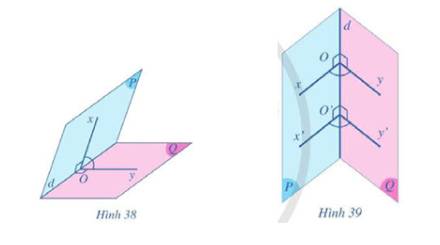

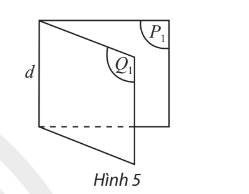



Trong \(\left( P \right)\) ta có:
\(\left. \begin{array}{l}Ox \bot d\\O'x' \bot d\end{array} \right\} \Rightarrow Ox\parallel O'x'\)
Trong \(\left( Q \right)\) ta có:
\(\left. \begin{array}{l}Oy \bot d\\O'y' \bot d\end{array} \right\} \Rightarrow Oy\parallel O'y'\)
Vậy \(\left( {Ox,Oy} \right) = \left( {O'x',O'y'} \right)\) hay số đo của hai góc \(xOy\) và \(x'Oy'\) bằng nhau.