Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) `[S,BC,O]`:
Góc phẳng nhị diện `[S,BC,O`] là góc giữa mặt phẳng `(SBC)` và mặt phẳng `(SBO)`. Vì hình chóp tứ giác đều, nên mặt phẳng `(SBC)` và mặt phẳng `(SBO)` là hai mặt phẳng vuông góc với nhau. Do đó, góc phẳng nhị diện `[S,BC,O]` là góc vuông.
b) `[C,SO,B]`:
Góc phẳng nhị diện `[C,SO,B]` là góc giữa mặt phẳng `(CSO)` và mặt phẳng `(CSB)`. Vì hình chóp tứ giác đều, nên mặt phẳng `(CSO)` và mặt phẳng `(CSB)` là hai mặt phẳng vuông góc với nhau. Do đó, góc phẳng nhị diện` [C,SO,B]` là góc vuông.

tham khảo
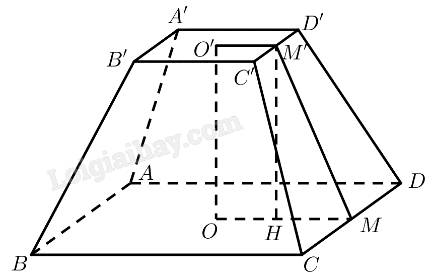
Mô hình hoá chân cột bằng gang bằng cụt chóp tứ giác đều \(ABCD.A'B'C'D'\) với \(O,O'\) là tâm của hai đáy.Vậy \(AB=2a,A'B'=a,OO'=2a\)
a)Gọi \(M,M'\) lần lượt là trung điểm của \(CD,C'D'.\)
\(A'B'C'D'\) là hình vuông \(\Rightarrow O'M\perp C'D\)
\(CDD'C\) là hình thang cân \(\Rightarrow MM'\perp C'D'\)
Vậy \(\widehat{MM'O}\) là góc phẳng nhị diện giữa mặt bên và đáy nhỏ,\(\widehat{M'MO}\) là góc phẳng nhị diện giữa mặt bên và đáy lớn.
Kẻ \(M'H\perp OM\left(H\in OM\right)\)
\(OMM'O'\) là hình chữ nhật
\(\Rightarrow OH=O'M'=\dfrac{a}{2},OM=a,MH=OM-OH=\dfrac{a}{2}\tan\widehat{M'MO}=\dfrac{M'H}{MH}=4\)
\(\Rightarrow\widehat{M'MO}=75,96^o\Rightarrow\widehat{MM'O'}=180^o-\widehat{M'MO}\\ =104,04^o\)
b)Diện tích đáy lớn là:\(S=AB^2=4a^{^2}\)
Diện tích đáy bé là:\(S'=A'B'^2=a^2\)
Thể tích hình chóp cụt là:
\(V_1=\dfrac{1}{3}h\left(S+\sqrt{SS'}+S'\right)\\ =\dfrac{1}{3}.2a\left(4a^2+\sqrt{4a^2.a^2}+a^2\right)=\dfrac{14a^3}{3}\)
Thể tích hình trụ rỗng là:\(V_2=\pi R^2h=\pi\left(\dfrac{a}{2}\right)^2.2a=\dfrac{\pi a^3}{2}\)
Thể tích chân cột là:\(V=V_1-V_2=\left(\dfrac{14}{3}-\dfrac{\pi}{2}\right)a^3\)

Do S.ABCD là chóp đều \(\Rightarrow BD\perp\left(SAC\right)\)
Mà BD là giao tuyến (MBD) và (ABCD)
\(\Rightarrow\widehat{MOC}\) là góc giữa (MBD) và (ABCD)
\(OC=\dfrac{AC}{2}=\dfrac{a\sqrt{2}}{2}\) ; \(MC=OM=\dfrac{1}{2}SC=\dfrac{a}{2}\)
Áp dụng định lý hàm cosin:
\(cos\widehat{MOC}=\dfrac{OM^2+OC^2-CM^2}{2OM.OC}=\dfrac{\sqrt{2}}{2}\)
\(\Rightarrow\widehat{MOC}=45^0\)

a: AC vuông góc BD
AC vuông góc SO
=>AC vuông góc (SBD)
=>SB vuông góc AC
mà AC vuông góc BD
nên AC vuông góc (SBD)
BD vuông góc AC
BD vuông góc SO
=>BD vuông góc (SAC)
=>BD vuông góc SA
b: Xét ΔACB có CO/CA=CI/CB
nên OI//AB
=>OI vuông góc BC
BC vuông góc OI
BC vuông góc SO
=>BC vuông góc (SOI)
=>(SBC) vuông góc (SOI)

Đáp án A.
Gọi H là hình chiếu của C trên SO và góc S O C ^ tù nên H nằm ngoài đoạn SO => CH ⊥ (SBD)
=> Góc tạo bởi SC và (SBD) là C S O ^
Lại có ![]()
![]()
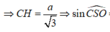
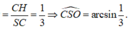


a) Kẻ \(C'H \bot OC\left( {H \in OC} \right)\)
là hình chữ nhật \( \Rightarrow OH = O'C' = a,OO'\parallel C'H\)
Mà \(OO' \bot \left( {ABCDEF} \right)\)
\(\begin{array}{l} \Rightarrow C'H \bot \left( {ABCDEF} \right)\\ \Rightarrow \left( {CC',\left( {ABCDEF} \right)} \right) = \left( {CC',CH} \right) = \widehat {C'CH}\end{array}\)
\(\begin{array}{l}HC = OC - O'C' = \frac{a}{2},C'H = OO' = a\\ \Rightarrow \tan \widehat {C'CH} = \frac{{C'H}}{{HC}} = 2 \Rightarrow \widehat {C'CH} \approx 63,{4^ \circ }\end{array}\)
Vậy \(\left( {CC',\left( {ABCDEF} \right)} \right) \approx 63,{4^ \circ }\)
b) Gọi \(M,M'\) lần lượt là trung điểm của \(AB,A'B'\).
\( \Rightarrow OM \bot AB,O'M' \bot A'B'\)
\(ABB'A'\) là hình thang cân \( \Rightarrow MM' \bot AB,MM' \bot A'B'\)
\( \Rightarrow \left[ {O,AB,A'} \right] = \widehat {OMM'},\left[ {O',A'B',A} \right] = \widehat {O'M'M}\)
Kẻ \(M'K \bot OM\left( {K \in OM} \right)\)
\(OO'M'K\) là hình chữ nhật \( \Rightarrow OK = O'K' = \frac{{A'B'\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{4},OO' = M'K = a\)
\(\begin{array}{l}OM = \frac{{AB\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{2},MK = OM - OK = \frac{{a\sqrt 3 }}{4}\\ \Rightarrow \tan \widehat {OMM'} = \frac{{M'K}}{{MK}} = \frac{4}{{\sqrt 3 }} \Rightarrow \widehat {OMM'} \approx 66,{6^ \circ }\\ \Rightarrow \widehat {O'M'M} = {180^ \circ } - \widehat {OMM'} = 113,{4^ \circ }\end{array}\)