Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

tham khảo:
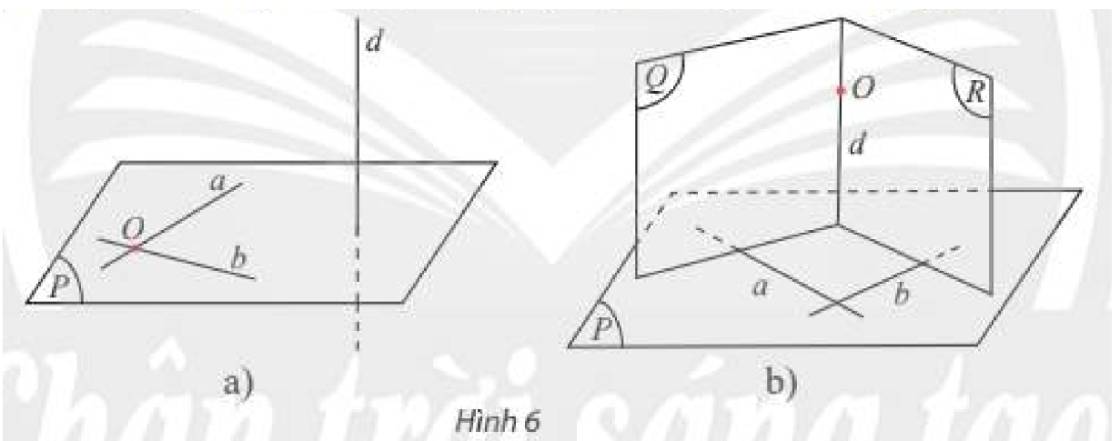
a) Vì đường thẳng d vuông góc hai đường thẳng cắt nhau a và b cùng nằm trong mặt phẳng (P) nên d⊥(P)
b) Vì a⊥(Q);d∈(Q) nên a⊥d
Vì b⊥(R),d∈(R) nên b⊥d
Vì đường thẳng d vuông góc hai đường thẳng cắt nhau a và b cùng nằm trong mặt phẳng (P) nên d⊥(P)

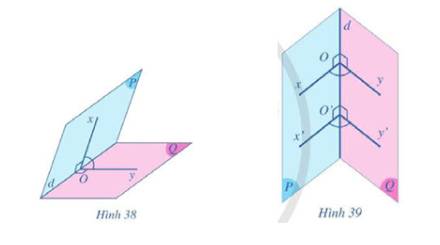
Trong \(\left( P \right)\) ta có:
\(\left. \begin{array}{l}Ox \bot d\\O'x' \bot d\end{array} \right\} \Rightarrow Ox\parallel O'x'\)
Trong \(\left( Q \right)\) ta có:
\(\left. \begin{array}{l}Oy \bot d\\O'y' \bot d\end{array} \right\} \Rightarrow Oy\parallel O'y'\)
Vậy \(\left( {Ox,Oy} \right) = \left( {O'x',O'y'} \right)\) hay số đo của hai góc \(xOy\) và \(x'Oy'\) bằng nhau.

tham khảo:
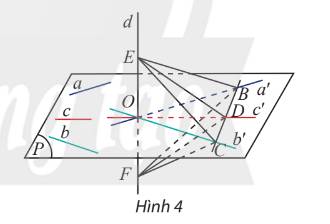
a) Vì a//a', d⊥a nên d⊥a′, Hay EF⊥OB
Tam giác EBF có OB⊥EF; O là trung điểm EF nên tam giác EBF cân tại B. Suy ra BE = BF
Tương tự ta chứng minh được CE = CF
Suy ra tam giác CEB bằng tam giác CFB
b) Vì tam giác CEB và CFB bằng nhau nên DE = DF
Nên tam giác DEF cân tại D có DO là trung tuyến nên DO⊥EF
Suy ra d⊥c

Ta có:
\(\left. \begin{array}{l}\left( Q \right)\parallel \left( R \right)\\\left( P \right) \cap \left( Q \right) = a'\\\left( P \right) \cap \left( R \right) = b'\end{array} \right\} \Rightarrow a'\parallel b'\)
Vậy nếu \(\left( Q \right)\parallel \left( R \right)\) thì \(a'\parallel b'\); nếu \(\left( Q \right) \equiv \left( R \right)\) thì \(a' \equiv b'\).

a) b // c; b ⊥ (P) ⇒ c ⊥ (P)
Mà a ⊥ (P)
a, c cùng đi qua điểm O
⇒ a trùng c.
b) Ta có b // c mà a trùng c nên a // b.

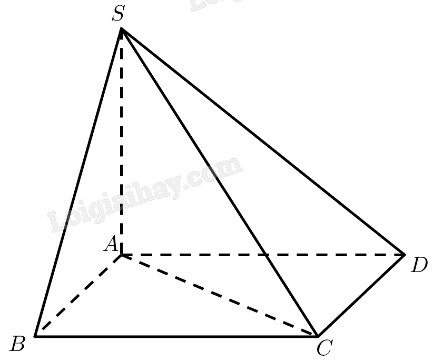
a) \(SA \bot \left( {ABCD} \right) \Rightarrow SA \bot AB,SA \bot A{\rm{D}}\)
Vậy \(\widehat {BA{\rm{D}}}\) là góc phẳng nhị diện của góc nhị diện \(\left[ {B,SA,D} \right]\)
\(ABCD\) là hình vuông \( \Rightarrow \widehat {BA{\rm{D}}} = {90^ \circ }\)
Vậy số đo của góc nhị diện \(\left[ {B,SA,D} \right]\) bằng \({90^ \circ }\).
b) \(SA \bot \left( {ABCD} \right) \Rightarrow SA \bot AB,SA \bot A{\rm{C}}\)
Vậy \(\widehat {BA{\rm{C}}}\) là góc phẳng nhị diện của góc nhị diện \(\left[ {B,SA,C} \right]\)
\(ABCD\) là hình vuông \( \Rightarrow \widehat {BA{\rm{C}}} = {45^ \circ }\)
Vậy số đo của góc nhị diện \(\left[ {B,SA,C} \right]\) bằng \({45^ \circ }\).

Do \(d\perp\left(ABC\right)\) nên \(MN\perp BC\)
\(\left\{{}\begin{matrix}MC\perp\left(BOH\right)\\BN\subset\left(BOH\right)\end{matrix}\right.\) \(\Rightarrow MC\perp BN\)
\(\left\{{}\begin{matrix}MB\perp\left(CHO\right)\\CN\subset\left(CHO\right)\end{matrix}\right.\)\(\Rightarrow MB\perp CN\)


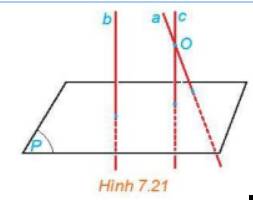

a: \(d\perp Ox;d\perp Oy\)
=>\(d\perp\left(Ox,Oy\right)\)
b: Số đo của \(\widehat{xOy}\) sẽ không đổi khi O di chuyển trên d
THAM KHẢO:
a) d⊥mp(Ox,Oy)
b) Khi O thay đổi trên d thì số đo góc \(\widehat{xOy}\)không đổi