Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi E là trung điểm AB \(\Rightarrow OE\perp AB\)
Do D là trung điểm BC \(\Rightarrow BD=\dfrac{1}{2}BC\) (1)
Do C đối xứng A qua M \(\Rightarrow AM=\dfrac{1}{2}AC\)
Do E là trung điểm AB \(\Rightarrow AE=\dfrac{1}{2}AB\)
\(\Rightarrow AM+AE=\dfrac{1}{2}AC+\dfrac{1}{2}AB\Rightarrow ME=\dfrac{1}{2}BC\) (2)
(1);(2) \(\Rightarrow BD=ME\)
Trong tam giác vuông OAE, do OA là cạnh huyền và OE là cạnh góc vuông \(\Rightarrow OE< OA\Rightarrow OE< r\)
Áp dụng định lý Pitago:
\(ME^2=OM^2-OE^2=d^2-OE^2>d^2-r^2\)
\(\Rightarrow BD^2>d^2-r^2\Rightarrow BD>\sqrt{\left(d-r\right)\left(d+r\right)}\)

a: Phải vì góc này tạo bởi tiếp tuyến MA và day cung AB
b: Xét ΔMOA vuông tại A có cosMOA=OA/OM=1/2
=>góc MOA=60 độ
sđ cung AB=2*60=120 độ
c: Xét (O) có
MA,MB là tiếp tuyến
=>MA=MB
mà OA=OB
nên OM là trung trực của AB
=>OM vuông góc AB tại H
=>MH*MO=MA^2
Xét ΔMAC và ΔMDA có
góc MAC=góc MDA
góc AMC chung
=>ΔMAC đồng dạng với ΔMDA
=>MA/MD=MC/MA
=>MA^2=MD*MC=MH*MO
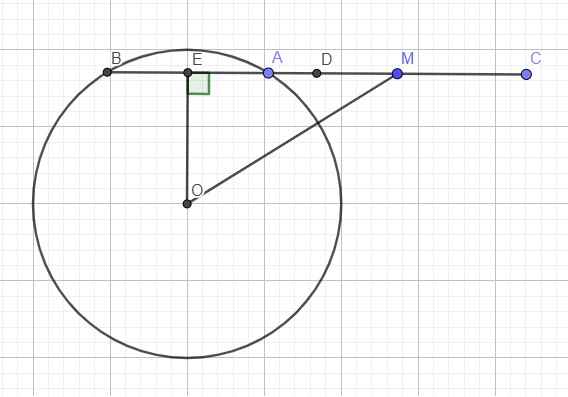
Xin lỗi các bạn. Đề bài đúng phải là so sánh BD với \(\sqrt{\left(d-r\right)\left(d+r\right)}\)
Gọi E là trung điểm AB \(\Rightarrow OE\perp AB\)
Do D là trung điểm BC \(\Rightarrow BD=\dfrac{1}{2}BC\) (1)
Do C đối xứng A qua M \(\Rightarrow AM=\dfrac{1}{2}AC\)
Do E là trung điểm AB \(\Rightarrow AE=\dfrac{1}{2}AB\)
\(\Rightarrow AM+AE=\dfrac{1}{2}AC+\dfrac{1}{2}AB\Rightarrow ME=\dfrac{1}{2}BC\) (2)
(1);(2) \(\Rightarrow BD=ME\)
Trong tam giác vuông OAE, do OA là cạnh huyền và OE là cạnh góc vuông \(\Rightarrow OE< OA\Rightarrow OE< r\)
Áp dụng định lý Pitago:
\(ME^2=OM^2-OE^2=d^2-OE^2>d^2-r^2\)
\(\Rightarrow BD^2>d^2-r^2\Rightarrow BD>\sqrt{\left(d-r\right)\left(d+r\right)}\)