Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đường tròn (C) tâm \(O\left(2;3\right)\) bán kính \(R=10\)
Gọi I là trung điểm AB \(\Rightarrow IO\perp AB\)
\(\Rightarrow IO=d\left(O;AB\right)=\dfrac{\left|3.2-4.3+1\right|}{\sqrt{3^2+4^2}}=1\)
Áp dụng định lý Pitago:
\(IA=\sqrt{OA^2-OA^2}=\sqrt{100-1}=3\sqrt{11}\)
\(\Rightarrow AB=2IA=6\sqrt{11}\)

Chọn B.
Vì đường tròn (C) cắt Δ tại hai điểm phân biệt A và B nên tọa độ điểm A và B là nghiệm của hệ phương trình:
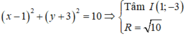
Gọi H là trung điểm của AB suy ra IH ⊥ AB ⇒ IH ⊥ Δ.
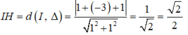
Xét tam giác AIH vuông tại H ta có:
A H 2 + I H 2 = A I 2 ⇒ A H 2 = A I 2 - I H 2
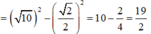
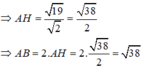

Đường tròn tâm \(I\left(1;-3\right)\) bán kính \(R=\sqrt{10}\)
Gọi H là trung điểm AB \(\Rightarrow IH\perp d\)
\(IH=d\left(I;d\right)=\frac{\left|1.1-3.1+1\right|}{\sqrt{1^2+1^2}}=\frac{1}{\sqrt{2}}\)
\(\Rightarrow AB=2IA=\sqrt{R^2-IH^2}=\sqrt{38}\)

(C) có tâm \(I\left(1;1\right)\) bán kính \(R=2\)
\(\Delta//d\Rightarrow\) phương trình \(\Delta\) có dạng: \(3x-4y+c=0\)
Áp dụng định lý Pitago: \(d\left(I;\Delta\right)=\sqrt{R^2-\left(\frac{AB}{2}\right)^2}=1\)
\(\Rightarrow\frac{\left|3.1-4.1+c\right|}{\sqrt{3^2+4^2}}=1\Leftrightarrow\left|c-1\right|=5\Rightarrow\left[{}\begin{matrix}c=6\\c=-4\end{matrix}\right.\)
Có 2 đường thẳng thỏa mãn: \(\left[{}\begin{matrix}3x-4y+6=0\\3x-4y-4=0\end{matrix}\right.\)
Do tính chất của đường tròn nên luôn có 2 đường thẳng đối xứng nhau qua tâm đường tròn thỏa mãn điều kiện bài toán, kiểu như trên hình, 2 dây cung cắt bởi 2 đường thẳng đối xứng qua tâm luôn dài bằng nhau
Chắc chắn cả 2 đáp án đều đúng, ko cái nào sai cả, nếu trong phương án chọn chỉ có 2 đáp án nằm riêng lẻ thì 1 là đáp án sai, 2 là bạn để ý kĩ lại dấu của 2 đáp án coi, có khi họ cho khác đi 1 chút xíu

1.
\(\left(C\right):x^2+y^2-2x-4=0\)
\(\Leftrightarrow\left(x-1\right)^2+y^2=5\)
Đường tròn \(\left(C\right)\) có tâm \(I=\left(1;0\right)\), bán kính \(R=\sqrt{5}\)
Phương trình đường thẳng \(d_1\) có dạng: \(x+y+m=0\left(m\in R\right)\)
Mà \(d_1\) tiếp xúc với \(\left(C\right)\Rightarrow d\left(I;d_1\right)=\dfrac{\left|1+m\right|}{\sqrt{2}}=\sqrt{5}\)
\(\Leftrightarrow\left|m+1\right|=\sqrt{10}\)
\(\Leftrightarrow m=-1\pm\sqrt{10}\)
\(\Rightarrow\left[{}\begin{matrix}d_1:x+y-1+\sqrt{10}=0\\d_1:x+y-1-\sqrt{10}=0\end{matrix}\right.\)
2.
Phương trình đường thẳng \(\Delta\) có dạng: \(x-y+m=0\left(m\in R\right)\)
Ta có: \(d\left(I;\Delta\right)=\sqrt{R^2-\dfrac{MN^2}{4}}=2\)
\(\Leftrightarrow\dfrac{\left|m+1\right|}{\sqrt{2}}=2\)
\(\Leftrightarrow m=-1\pm2\sqrt{2}\)
\(\Rightarrow\left[{}\begin{matrix}\Delta:x-y+1+2\sqrt{2}=0\\\Delta:x-y+1-2\sqrt{2}=0\end{matrix}\right.\)

Lời giải:
Gọi $I(-1;3)$ là tâm của đường tròn. Kẻ $IH\perp (\Delta)$ thì $H$ chính là trung điểm của $AB$.
Ta có:
\(IH=d(I,\Delta)=\frac{|-1-2.3+5|}{\sqrt{1^2+(-2)^2}}=\frac{2\sqrt{5}}{5}\)
\(IA=R=\sqrt{20}\)
Áp dụng định lý Pitago: \(AH=\sqrt{IA^2-IH^2}=\sqrt{20-(\frac{2\sqrt{5}}{5})^2}=\frac{4\sqrt{30}}{5}\)
\(\Rightarrow AB=2AH=\frac{8\sqrt{30}}{5}\)
Hình vẽ:
