Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

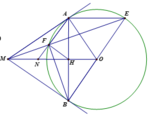
1) Chứng minh: Tứ giác MAOB nội tiếp một đường tròn
Vẽ được các yếu tố để chứng minh phần (1).
Ta có M B O ^ = 90 0 , M A O ^ = 90 0 (theo t/c của tiếp tuyến và bán kính)
Suy ra: M A O ^ + M B O ^ = 180 0 .Vậy tứ giác MAOB nội tiếp đường tròn.
2) Chứng minh: MN2 = NF. NA và MN = NH
Ta có A E / / M O ⇒ A E M ^ = E M N ^ mà A E M ^ = M A F ^ ⇒ E M N ^ = M A F ^
Δ N M F v à Δ N A M có: M N A ^ chung; E M N ^ = M A F ^
nên Δ N M F đồng dạng với Δ N A M
⇒ N M N F = N A N M ⇒ N M 2 = N F . N A 1
Mặt khác có: A B F ^ = A E F ^ ⇒ A B F ^ = E M N ^ h a y H B F ^ = F M H ^
=> MFHB là tứ giác nội tiếp
⇒ F H M ^ = F B M ^ = F A B ^ h a y F H N ^ = N A H ^
Xét Δ N H F & Δ N A H c ó A N H ^ c h u n g ; N H F ^ = N A H ^
=> Δ N M F đồng dạng Δ N A H ⇒ ⇒ N H N F = N A N H ⇒ N H 2 = N F . N A 2
Từ (1) và (2) ta có NH = HM
3) Chứng minh: H B 2 H F 2 − EF M F = 1 .
Xét Δ M AF và Δ M E A có: A M E ^ chung, M A F ^ = M E A ^
suy ra Δ M AF đồng dạng với Δ M E A
⇒ M E M A = M A M F = A E A F ⇒ M E M F = A E 2 A F 2 (3)
Vì MFHB là tứ giác nội tiếp ⇒ M F B ^ = M H B ^ = 90 0 ⇒ B F E ^ = 90 0 và A F H ^ = A H N ^ = 90 0 ⇒ A F E ^ = B F H ^
Δ A E F và Δ H B F có: E F A ^ = B F H ^ ; F E A ^ = F B A ^
suy ra Δ A E F ~ Δ H B F
⇒ A E A F = H B H F ⇒ A E 2 A F 2 = H B 2 H F 2 (4)
Từ (3) và (4) ta có M E M F = H B 2 H F 2 ⇔ M F + F E M F = H B 2 H F 2 ⇔ 1 + F E M F = H B 2 H F 2 ⇔ H B 2 H F 2 − F E M F = 1

Ta có: \(\widehat{OAM}=\widehat{OBM}=90^o\)(Vì AM là đường trung tuyến của (O))
\(\Rightarrow\widehat{OAM}+\widehat{OBM}=180^o\)
=> Tứ giác MAOB nội tiếp
Theo tính chất tiếp tuyến cắt nhau ta có MA=MB; OA=OB
=> MO là đường trung trực của AB
=> MO _|_ AB tại H
Mà \(\widehat{BAE}=90^o\)hay AE _|_ AB. Do đó AE // MO
Vì AE // MO và MA là tiếp tuyến của (O) nên \(\widehat{NMF}=\widehat{AEF}=\widehat{NAM}\)
=> Tam giác NMA đồng dạng tam giác NFM (gg)
=> \(\frac{NM}{NF}=\frac{NA}{NM}\)\(\Rightarrow NM^2=AN\cdot NF\left(1\right)\)
Ta có: \(\widehat{MFB}=\widehat{MHB}=90^o\)=> Tứ giác MFHB nội tiếp
\(\Rightarrow\widehat{FHN}=\widehat{FBM}\)mà \(\widehat{FBM}=\widehat{NAH}\)
\(\Rightarrow\widehat{NAH}=\widehat{FHN}\)
\(\Rightarrow\Delta NAH\)đồng dạng \(\Delta NHF\left(g.g\right)\)
\(\Rightarrow\frac{NA}{NH}=\frac{NH}{NF}\Rightarrow NH^2=NA\cdot NF\left(2\right)\)
(1)(2) => NM2=NH2 => MN=NH (đpcm)


a) Chứng minh tứ giác MAOB nội tiếp đường tròn
Xét tứ giác MAOB có: \(\widehat{MAO}=90\text{°}\) (MA là tiếp tuyến của (O)); \(\widehat{MBO}=90\text{°}\) (MB là tiếp tuyến của (O))
→ \(\widehat{MAO}+\widehat{MBO}=180\text{°}\)
mà \(\widehat{MAO}\) và \(\widehat{MBO}\) là hai góc đối nhau
→ Tứ giác MAOB nội tiếp (dhnb) (đpcm)
b) Chứng minh MA.AB = 2MH.AO
Ta có: OA = OB (A, B ∈ (O))
→ O thuộc đường trung trực của AB (1)
Lại có: MA = MB (Tính chất hai tiếp tuyến cắt nhau)
→ M thuộc đường trung trực của AB (2)
Từ (1) và (2) → OM là đường trung trực của AB
→ OM ⊥ AB tại H và H là trung điểm của AB
→ \(\widehat{MHA}=90\text{°}\) và AB = 2AH
Xét ∆MAO và ∆MHA có: \(\widehat{MAO}=\widehat{MHA}=90\text{°}\); \(\widehat{M}\) chung
→ ∆MAO ∼ ∆MHA (g.g) → \(\dfrac{MA}{MH}=\dfrac{AO}{HA}\) (cặp cạnh tương ứng)
→ MA.HA = MH.AO
→ 2MA.HA = 2MH.AO
Mà AB = 2AH (cmt) → MA.AB = 2MH.AO (đpcm)
MA.HA = MH.AO
→ 2MA.HA = 2MH.AO
Mà AB = 2AH (cmt) → MA.AB = 2MH.AO (đpcm)
chỗ đây ko hiểu ;;;-;;;

M O A B E N H F
Ta có: AE // MO => ^AEM=^OME (So le trong) hay ^AEF=^HMF
Mà ^AEF=^FBH (=^FBA) (Cung chắn cung AF) => ^HMF=^FBH
=> Tứ giác MFHB nội tiếp đường tròn.
=> ^BFH=^BMH. Mà ^BMH=^ABO (Cùng phụ với ^MBH) => ^BFH=^ABO.
Dễ thấy MO vuông góc AB tại H, do AE//MO => AE vuông góc AB (Q/h song song, vg góc)
Ta thấy 3 điểm B;A;E cùng nằm trên (O) và ^BAE=900 => 3 điểm B;O;E thẳng hàng
=> ^ABO=^ABE. Do đó ^BFH=^ABE.
Lại có: ^ABE=^AFE (Cùng chắn cung AE) và ^AFE=^MFN (Đối đỉnh) => ^BFH=^MFN.
Xét \(\Delta\)FHB và \(\Delta\)FNM: ^BFH=^MFN; ^FBH=^FMN
=> \(\Delta\)FHB ~ \(\Delta\)FNM (g.g) => \(\frac{BH}{MN}=\frac{FH}{FN}\)(1)
^MFN + ^NFB = 900 => ^BFH + ^NFB = 900 => ^NFH = 900
=> \(\Delta\)NFH ~ \(\Delta\)HFA (g.g) => \(\frac{AH}{NH}=\frac{HF}{FN}\)(2)
Từ (1) và (2) => \(\frac{BH}{MN}=\frac{AH}{NH}\). Mà AH=BH => MN=NH, thay vào hệ thức:
\(\frac{HB}{MN}=\frac{HF}{NF}\Leftrightarrow\frac{HB}{HF}=\frac{MN}{NF}\)(Do \(\Delta\)BHF ~ \(\Delta\)MNF)
=> \(\frac{HB}{HF}=\frac{NH}{NF}\Leftrightarrow\frac{HB^2}{HF^2}=\frac{NH^2}{NF^2}\)
Áp dụng hệ quả ĐL Thales: \(\frac{EF}{MF}=\frac{AF}{NF}\)
\(\Rightarrow\frac{HB^2}{HF^2}-\frac{EF}{MF}=\frac{NH^2}{NF^2}-\frac{AF}{NF}=\frac{NH^2-AF.NF}{NF^2}\)
Dễ có: \(\Delta\)NFH ~ \(\Delta\)NHA => \(\frac{NF}{NH}=\frac{NH}{NA}\Rightarrow NH^2=NF.NA\)
\(\Rightarrow NH^2-AF.NF=NF.NA-AF.NF=NF.\left(NA-AF\right)=NF.NF=NF^2\)
\(\Rightarrow\frac{NH^2-AF.NF}{NF^2}=\frac{NF^2}{NF^2}=1\Rightarrow\)\(\frac{HB^2}{HF^2}-\frac{EF}{MF}=1.\)(đpcm).
GƠI Ý PHẦN C: Như ý b ta có MN^2=NF.NA
bẠN HÃY CỐ ÉP NH^2=NF.NA . => ĐPCM.
( Chúc bạn học tốt , thân! <3 )