Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
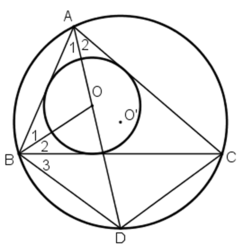
Do O là tâm đường tròn nội tiếp tam giác ABC nên O là giao điểm của ba đường phân giác của tam giác ABC.
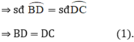
(hai cung bằng nhau căng hai dây bằng nhau).
+ 
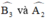đều là các góc nội tiếp chắn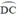 
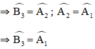
ΔOAB có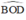 
là góc ngoài của tam giác
Từ (1) và (2) suy ra DB = DC = DO.
Vậy chọn đáp án D.
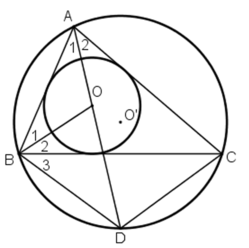
Do O là tâm đường tròn nội tiếp tam giác ABC nên O là giao điểm của ba đường phân giác của tam giác ABC.
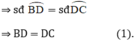
(hai cung bằng nhau căng hai dây bằng nhau).
+ 
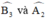đều là các góc nội tiếp chắn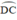 
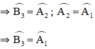
ΔOAB có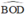 
là góc ngoài của tam giác
Từ (1) và (2) suy ra DB = DC = DO.
Vậy chọn đáp án D.
Hướng dẫn làm bài:
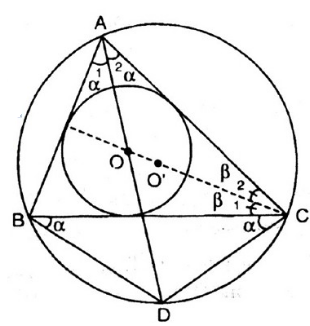
Vì AC vad BC tiếp xúc với đường tròn (O), AD đi qua O nên ta có:
ˆCAD=ˆBAD=αCAD^=BAD^=α (vì tâm đường tròn nội tiếp trong tam giác là giao điểm của ba đường phân giác trong tam giác)
⇒ cung CD = cung DB ⇒CD = DB (*)
Tương tự, CO là tia phân giác của góc C nên:
ˆACO=ˆBCO=βACO^=BCO^=β
Mặt khác: ˆDCO=ˆDCB+ˆBCO=α+β(1)(doˆBAD=ˆBCDDCO^=DCB^+BCO^=α+β(1)(doBAD^=BCD^
Ta có: ˆCODCOD^ là góc ngoài của ∆ AOC nên
ˆCOD=ˆOAC+ˆOCA=β+α(2)COD^=OAC^+OCA^=β+α(2)
Từ (1) và (2) ta có: ˆOCD=ˆCODOCD^=COD^
Vậy ∆DOC cân tại D (**)
Từ (*) và (**) suy ra CD = OD = BD
Chọn đáp án D
O A B C H D I K E F
b) Ta thấy (O) giao (I) tại 2 điểm B và D => BD vuông góc OI (tại K) => ^OKB=900.
Xét đường tròn (I) đường kính AB có H thuộc cung AB => AH vuông góc HB hay AH vuông góc BC (1)
AB và AC là 2 tiếp tuyến của (O) => \(\Delta\)ABC cân tại A. Mà AO là phân giác ^BAC
=> AO vuông góc BC (2)
Từ (1) và (2) => A;H;O thẳng hàng => ^OHB=900.
Xét tứ giác BOHK: ^OKB=^OHB=900 => Tứ giác BOHK nội tiếp đường tròn đường kính OB
=> ^OKH = ^OBH. Lại có ^OBH=^OAB (Cùng phụ ^HBA) => ^OKH = ^OAB
Hay ^OKH = ^HAI. Mà ^OKH + ^KHI = 1800 nên ^HAI + ^KHI = 1800
=> Tứ giác AIKH nội tiếp đường tròn (đpcm).
b) Dễ thấy OI là trung trực của BD và OI cắt BD tại K => K là trung điểm của BD
\(\Delta\)ABC cân đỉnh A có đường phân giác AH => H là trung điểm BC
Từ đó suy ra HK là đường trung bình của \(\Delta\)BDC
=> HK//CD => ^HKD + ^CDK = 1800 (3). Đồng thời \(\frac{HK}{CD}=\frac{1}{2}\)
Tương tự KI là đường trg bình của \(\Delta\)BAD => KI//AD => ^DKI + ^ADK = 1800 (4) Và \(\frac{IK}{AD}=\frac{1}{2}\)
Cộng (3) với (4) => ^KHD + ^KDI + ^CDK + ^ ADK = 3600
<=> ^HKI = 3600 - (^CDK + ^ADK) => ^HKI = ^CDA.
Xét \(\Delta\)HKI và \(\Delta\)CDA: ^HKI=^CDA; \(\frac{HK}{CD}=\frac{IK}{AD}=\frac{1}{2}\)=> \(\Delta\)HKI ~ \(\Delta\)CDA (c.g.c)
=> ^HIK = ^CAD. Mặt khác: ^CAD = ^DBE (Cùng chắn cung DE) => ^HIK=^DBE.
Mà tứ giác AIKH nội tiếp đường tròn => ^HIK=^HAK = >^DBE=^HAK hay ^KBF=^FAK
=> Tứ giác BKFA nội tiếp đường tròn => Đường tròn ngoại tiếp tam giác ABF đi qua điểm K (đpcm).
O A B C D E H F
a) Do D thuộc đường tròn (O), AB là đường kính nên \(\widehat{BDC}=90^o\Rightarrow BD\perp AC\)
Xét tam giác vuông ABC, đường cao BD ta có:
\(AB^2=AD.AC\) (Hệ thức lượng)
b) Xét tam giác BEC có O là trung điểm BC; OH // CE nên OH là đường trung bình của tam giác. Vậy nên H là trung điểm BE.
Ta có OH // CE mà CE vuông góc AB nên \(OH\perp BE\)
Xét tam giác ABE có AH là trung tuyến đồng thời đường cao nên nó là tam giác cân.
Hay AB = AE.
Từ đó ta có \(\Delta ABO=\Delta AEO\left(c-c-c\right)\Rightarrow\widehat{OEA}=\widehat{OBA}=90^o\)
Vậy AE là tiếp tuyến của đường tròn (O)
c) Xét tam giác vuông OBA đường cao BH, ta có:
\(OB^2=OH.OA\) (Hệ thức lượng)
\(\Rightarrow OC^2=OH.OA\Rightarrow\frac{OH}{OC}=\frac{OC}{OA}\)
Vậy nên \(\Delta OHC\sim\Delta OCA\left(c-g-c\right)\Rightarrow\widehat{OHC}=\widehat{OCA}\)
d) Ta thấy \(\widehat{OCF}=\widehat{FCE}\left(=\widehat{OFC}\right)\)
Lại có \(\widehat{OCH}=\widehat{ACE}\left(=\widehat{OAC}\right)\)
Nên \(\widehat{HCF}=\widehat{FCA}\) hay CF là phân giác góc HCA.
Xét tam giác HCA, áp dụng tính chất đường phân giác trong tam giác, ta có:
\(\frac{HF}{FA}=\frac{HC}{CA}\Rightarrow FA.HC=HF.CA\left(đpcm\right)\)
ở phần c còn cạnh nào nữa để 2 tam giác đấy đồng dạng vậy cậu
E C A D B
Ta có: tỨ giác OCEA nội tiếp
=> \(\widehat{OCA}=\widehat{OEA}\)(1)
Vì OC=OB
=> Tam giác OBC cân
=> \(\widehat{OCA}=\widehat{OCB}=\widehat{OBC}\)(2)
Tứ giác ODAB nội tiếp
=> \(\widehat{ODA}=\widehat{OBC}\)( cùng bù với góc OBA) (3)
Từ (1), (2), (3)
=> \(\widehat{ODA}=\widehat{OEA}\)
=> Tam giác ODE cân có OA là đươngcao
=> OA là đường trung tuyến
=> A là trung điểm của DE