Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

R1ntR2
\(=>R1+R2=100\Omega\)(1)
R1//R2
\(=>R_{td}=\dfrac{R1.R2}{R1+R2}=\dfrac{R1.R2}{100}=16\)
=>R1.R2=1600(2)
Từ (1)(2)
=> R1=20 \(\Omega\)
R2=80\(\Omega\)

- Điện trở tương đương của mạch khi mắc R1 nối tiếp với R2 là :
\(Rnt=\frac{Unt}{Int}=\frac{6}{0,24}=25\left(ôm\right)\)
hay R1 + R2 = 25 (Ω) (1)
- Điện trở tương đương của mạch khi mắc R1 song song với R2 là :
\(R_{ss}=\frac{U_{ss}}{I_{ss}}=\frac{6}{1}=1\)(Ω)
hay \(\frac{R_1.R_2}{R_1+R_2}=6\left(ôm\right)\)
-> R1.R2=6.(R1+R2)=6.25 hay R1.R2=150 (Ω) (2)
Giải hệ phương trình (1) và (2) ta được :
\(\begin{cases}R_1=15\left(\Omega\right),R_2=10\left(\Omega\right)\\R_1=10\left(\Omega\right),R_2=15\left(\Omega\right)\end{cases}\)
Vậy nếu R1=15(Ω) thì R2=10(Ω) , R1=10(Ω) thì R2=15(Ω)

Làm bài khó trước
Bài 2 :
Điện trở tương đương của n đoạn mạch song song là :
\(\dfrac{1}{R_{tđ}}=\dfrac{1}{R_1}+\dfrac{1}{R_2}+...+\dfrac{1}{R_n}\)
Các giá trị \(R_{tđ},R_1,R_2,...\)có giá trị dương nên:
\(\dfrac{1}{R_{tđ}}>\dfrac{1}{R_{R_1}}=>R_{tđ}< R_1\)
\(\dfrac{1}{R_{tđ}}>\dfrac{1}{R_2}=>R_{tđ}< R_2\)
\(........\)
\(\dfrac{1}{R_{tđ}}>\dfrac{1}{R_n}=>R_{tđ}< R_n\)
Rtđ của đoạn mạch song song nhau thì nhỏ hơn mỗi điện trở thành phần .
Bài 1 :
a, \(R_{tđ}=R_1+R_2=\dfrac{U}{I}=\dfrac{1,2}{0,12}=10\Omega\)
b,
Ta có : \(R_1\)//\(R_2\)
\(U_1=U_2\)
\(I_1.R_1=I_2.R_2\)
Mà \(I_1=1,5I_2\)
\(1,5I_2.R_1=I_2.R_2\)
\(=>1,5R_1=R_2\left(1\right)\)
Mặt khác ta có ; \(R=R_1+R_2=10\left(2\right)\)
Từ (1) và (2) có ;
\(R_1+1,5R_1=10\)
\(2,5R_1=10=>R_1=4\Omega\)
\(R_2=6\Omega\)
Vậy ...

Theo bài ra ta có ;
\(R_1+R_2=2.\left(\dfrac{R_1.R_2}{R_1+R_2}\right)\)
\(\Leftrightarrow R_1+R_2=\dfrac{2R_1.R_2}{R_1+R_2}\)
\(\Leftrightarrow\left(R_1+R_2\right)^2=2R_1.R_2\)
\(\Leftrightarrow R_1^2+R_2^2=0\)
Thể là đề sai hả V;
Mình cũng ko bt bạn có thể xem lại đề ko

gọi R1,R2 lần lượt là x,y(ôm)
->hệ pt: \(\left\{{}\begin{matrix}x+y=100\\\dfrac{xy}{x+y}=16\end{matrix}\right.< =>\left\{{}\begin{matrix}y=100-x\left(1\right)\\\dfrac{x\left(100-x\right)}{x+100-x}=16\left(2\right)\end{matrix}\right.\)
giải pt(2)
\(=>\dfrac{100x-x^2}{100}=16< =>-x^2+100x-1600=0\)
\(\Delta=100^2-4\left(-1600\right)\left(-1\right)=3600>0\)
\(=>\left[{}\begin{matrix}x1=\dfrac{-100+60}{-2}=20\\x2=\dfrac{-100-60}{-2}=80\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}y1=80\\y2=20\end{matrix}\right.\)
vậy (R1;R2)={(20;80),(80;20)}

Khi mắc nối tiếp thì điện trở tương đương là 9Ω nên ta có:
\(R_{\text{tđ}}=R_1+R_2=9\Omega\) (1)
\(\Rightarrow R_2=9-R_1\left(2\right)\)
Khi mắt nối tiếp thì điện trở tương đương là 2Ω nên ta có:
\(R_{\text{tđ}}=\dfrac{R_1R_2}{R_1+R_2}=2\Omega\)
\(\Rightarrow R_1+R_2=\dfrac{R_1R_2}{2}\) (3)
Thay (3) vào (1) ta có:
\(\Rightarrow9=\dfrac{R_1R_2}{2}\Rightarrow R_1R_2=18\) (44)
Thay (3) vào (4) ta có:
\(R_1\cdot\left(9-R_1\right)=18\)
\(\Rightarrow9R_1-R^2_1=18\)
\(\Rightarrow R^2_1-9R_1+18=0\)
\(\Rightarrow\left[{}\begin{matrix}R_1=3\Omega\\R_1=6\Omega\end{matrix}\right.\)
TH1: \(R_1=3\Omega\)
\(\Rightarrow R_2=9-3=6\Omega\)
TH2: \(R_2=6\Omega\)
\(\Rightarrow R_2=9-6=3\Omega\)

1. a. Theo ht 4' trg đm //, ta có: Rtđ= (R1.R2)/(R1+R2)= (3.6)/(3+6)=2 ôm
b.Theo ĐL ôm, ta có: I= U/Rtđ=24/2=12 A
I1=U/R1=24/3=8 ôm
I2=U/R2=24/6=4 ôm

Đáp án B
Với R 1 = R 2 = r suy ra R n t = R 1 + R 2 = 2 r
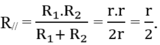
Từ đó ta thấy R n t = 4 R / / .

Mình làm vắn tắt, bạn trình bày rồi diễn giải ra một chút nhé
a, Vì R1 mắc nối tiếp R2
=>Rtđ=R1+R2=8+12=20Ω
CĐDD qua mạch chính:
\(I_{AB}=\frac{U_{AB}}{R_{AB}}=\frac{24}{20}=1,2\Omega\)
b, Đổi 10 phút = 600s
=>Q = \(Pt=UIt=24.1,2.600=17280\left(J\right)\)
c, Vì R3//R2
=>\(R_{23}=\frac{R_2.R_3}{R_2+R_3}=\frac{12.10}{12+10}=\frac{60}{11}\Omega\)
R1 nối tiếp R23
=> Rtđ=R1+R23=8+60/11 \(\approx13,45\Omega\)
R1 R2 R3 U A B 24V
Mình nghĩ vậy, có gì sai các bạn khác, thầy, cô đóng góp ý kiến sửa giúp mình nhé
Khi mắc nối tiếp thì
\(R_{nt}=R_1+R_2=100\) Ω
Khi mắc song song thì
\(R_{ss}=\frac{R_1R_2}{R_1+R_2}=16\) Ω
\(\Rightarrow\left\{{}\begin{matrix}R_1+R_2=100\\R_1R_2=1600\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}R_1=20\Omega\\R_2=80\Omega\end{matrix}\right.\)
tại sao `R_{1}R_{2}=1600` vậy ạ