Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
nAl2O3=10.2:102=0.1(mol)
PTHH:Al2O3+6HCl->2AlCl3+3H2O
theo pthh:nHCl:nAl2O3=6->nHCl=6*0.1=0.6(mol)
mHCl=0.6*36.5=21.9(g)
mdd HCl=21.9*100:14.6=150(g)
theo pthh:nAlCl3:nAl2O3=2->nAlCl3=0.1*2=0.2(mol)
mAlCl3=0.2*133.5=26.7(g)
mdd sau phản ứng:10.2+150=160.2
C%=26.7:160.2*100=16.7%
Câu 1:
Khối lượng CaO: 
Số mol CaO:
Pt:
số mol Ca (OH)2
Vậy khối lượng Ca(OH)2tạo thành: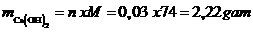
Vậy mct = 2,22 gam
Mà 
Vậy nồng độ phần trăm Ca(OH)2: 
Câu 2:
+ Khối lượng riêng 
khối lượng dd H2SO4 là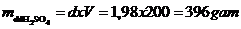 
+ 
Số mol CuO: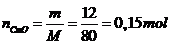 
Pt: 
Khối lượng 
Vậy khối lượng chất tan: mct = 24 gam
Mà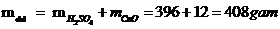 
Vậy nồng độ phần trăm: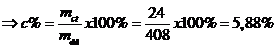 
Theo đề bài ta có : ⎧⎪ ⎪ ⎪⎨⎪ ⎪ ⎪⎩VddH2O4=601,2=50(ml)nNaOH=20.20100.40=0,1(mol){VddH2O4=601,2=50(ml)nNaOH=20.20100.40=0,1(mol)
nFe = 1,68/56 = 0,03 mol
a) Ta có PTHH :
2NaOH + H2SO4 -> Na2SO4 + 2H2O
0,1mol......0,05mol
=> CMH2SO4 = 0,05/0,05=1(M)
a) H2SO4+BaCl2---->BaSO4+2HCl
b) n\(_{H2SO4}=\frac{200.9,8}{100.98}=0,2\left(mol\right)\)
n\(_{BaCl2}=\frac{800.6,5}{100.208}=0,25\left(mol\right)\)
=> BaCl2 dư
Theo pthh
n\(_{BaSO4}=n_{H2SO4}=0,2\left(mol\right)\)
m\(_{BaSO4}=0,2.233=46,6\left(g\right)\)
m ddsau pư=800+200-46,6=953,4(g)
Theo pthh
n\(_{BaCl2}=n_{H2SO4}=0,2\left(mol\right)\)
n BaCl2 dư=0,25-0,2=0,05(mol)
C% BaCl2=\(\frac{0,05.208}{953,4}.100\%=1,09\%\)
Theo pthh
n\(_{HCl}=2n_{H2SO4}=0,2\left(mol\right)\)
C% HCl=\(\frac{0,2.36,5}{953,4}.100\%=0,77\%\%\)
\(\text{h2so4 + bacl2 = baso4 + h2o}\)
Ta có :
\(\text{n h2so4 = 0,2 mol}\)
\(\text{n bacl2 = 0,25 mol }\)
theo pthh thì n h2so4 = n bacl2
\(\text{mà n bacl2 có > n h2so4}\)
--> h2so4 hết, còn bacl2 dư 0,05 mol
\(\text{m kết tủa = m baso4 = 0,2.233= 46,6g}\)
dd sau pứ là bacl2 dư 0,05mol
\(\text{m dd sau pứ = 200 + 800- 46,6 = 753,4g}\)
\(\text{--> C% Bacl2 = 0,05.208÷753,4.100%= 1,38%}\)
a)
PTHH :
\(Zn+H_2SO_4\rightarrow ZnSO_4+H_2\)
b)
\(n_{Zn}=\dfrac{6,5}{65}=0,1\left(mol\right)\)
\(\Rightarrow n_{H_2SO_4}=0,1\left(mol\right)\)
\(\Rightarrow m_{\text{dd}H_2SO_4}=\dfrac{0,1\cdot98}{9,8\%}=100\left(g\right)\)
c)
\(m_{\text{dd}\left(sau\right)}=100+6,5-0,1.2=106,3\left(g\right)\)
\(\Rightarrow C\%_{\text{dd}\left(sau\right)}=\dfrac{0,1\cdot161}{106,3}\cdot100\%=15,15\left(\%\right)\)