Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Khi một tam giác có đường trung tuyến đồng thời là đường phân giác thì đó là tam giác cân.
Ở đây tam giác ABC có AM là trung tuyến đồng thời là phân giác vậy
=> tam giác ABC là tam giác cân (tính chất tam giác cân)
Ta có hình vẽ :
A B C M H
Trên tia đổi của tia MA lấy điểm H sao cho MA=MH
Xét \(\Delta MBH\) và \(\Delta MCA\) có:
\(\left\{{}\begin{matrix}AM=HM\left(theocachve\right)\\\widehat{BMH}=\widehat{CMA\left(\text{đ}^2\right)}\\BM=CM\left(AMlatrungtuyen\right)\end{matrix}\right.\)
=> \(\Delta MBH\) = \(\Delta MCA\) (c.g.c)
=> +) BH=CA ( hai cạnh tương ứng) (1)
+) \(\widehat{BHM}=\widehat{CAM}\) ( hai góc tương ứng ) (2)
Ta lại có:
AM là phân giác => \(\widehat{BAM}=\widehat{MAC}\) (3)
Từ (2) và (3) suy ra: \(\widehat{BAM}=\widehat{MHB}\)
=> \(\Delta HBA\) là tam giác cân ( vì có hai góc ở đáy bằng nhau )
=> AB=HB ( hai cạnh bên của tam giác cân ) (4)
Từ (1) và (4) suy ra :
AB=AC
=> \(\Delta ABC\) là tam giác cân ( vì có hai cạnh trong tam giác bằng nhau )
( đ.p.c.m )

Xét ΔABC có
AM là đường trung tuyến
AM là đường phân giác
Do đó: ΔABC cân tại A
\(\text{Xét }\Delta ABC\text{ có:}\)
\(\left\{{}\begin{matrix}AM\text{ là đường phân giác(gt)}\\AM\text{ là đường trung tuyến(gt)}\end{matrix}\right.\)
\(\Rightarrow\Delta ABC\text{ cân tại A}\)

A B C D Cả 4 câu đều là 1 hình như thế này, chỉ có kí hiệu khác nhau, bạn tự dựa vào nội dung câu hỏi mà kí hiệu lên hình nhé.
Câu 1:
Xét tam giác ABD và tam giác ACD:
ADB= ADC =90o
AD chung
DB= DC
=> tam giác ABD = tam giác ACD (2 cạnh góc vuông)
=> góc B = góc C (2 góc tương ứng)
Vậy tam giác ABC cân
Câu 2:
Chứng minh y chang câu 1
Câu 3:
Xét tam giác ABD và tam giác ACD:
ADB= ADC =90o
AD chung
BAD = CAD
=> tam giác ABD = tam giác ACD (cạnh góc vuông_ góc nhọn)
=> góc B = góc C (2 góc tương ứng)
Vậy tam giác ABC cân
Câu 4:
Chứng minh giống hệt câu 3.

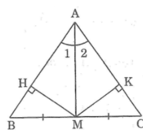
Kẻ MH ⊥ AB, MK ⊥ AC
Vì AM là tia phân giác của ∠(BAC) nên MH = MK (tính chất tia phân giác)
Xét hai tam giác MHB và MKC, ta có:
∠(MHB) = ∠(MKC) = 90º
MH = MK (chứng minh trên)
MB = MC (gt)
Suy ra: ΔMHB = ΔMKC (cạnh huyền, cạnh góc vuông)
Suy ra: ∠B = ∠C (hai góc tương ứng)
Vậy tam giác ABC cân tại A.

Câu 1 : ( mình đặt cho dễ viết nha )
Vì \(\Delta\)ABC vuông tại A ( gt )
=> \(\widehat{ABC}+\widehat{ACB}=90^o\)( vì trong tam giác vuông hai góc nhọn phụ nhau )
=> \(\hept{\begin{cases}\widehat{ABC}=90^o-\widehat{ACB}\\\widehat{ACB}=90^o-\widehat{ABC}\end{cases}}\)mà ABC , ACB > 0
=> 90o > ACB , 90o > ABC
hay BAC > ACB , BAC > ABC
Xét tam giác abc có BAC > ACB , BAC > ABC ( CMt )
=> BC là cạnh lớn nhất trong tam giác ( quan hệ giữa góc và cạnh đối diện trong tam giác ) ( dpcm )
Cạnh đối diện với góc vuông gọi là cạnh huyền. Hai cạnh kề với góc vuông là cạnh bên (hay còn gọi là cạnh góc vuông). Cạnh a có thể xem là kề với góc B và đối góc A, trong khi cạnh b kề góc A và đối góc B.
Nếu chiều dài của ba cạnh là các số nguyên, tam giác được gọi là tam giác Pythagore và chiều dài ba cạnh của nó được gọi chung là Bộ ba số Pythagore.
Ví dụ nè tam giác ABC vuông tại A nha
=) góc A = 90 độ
Vì tam giác ABC vuông tại A
=) góc B + góc C = 90 độ
=) góc A > góc B và góc A > góc C
=) góc A là góc lớn nhất
=) BC là cạnh lớn nhất ( ...... )

Kẻ MD vuông góc với AB, ME vuông góc với AC
Xét ΔADM vuông tại D và ΔAEM vuông tại E có
AM chung
\(\widehat{DAM}=\widehat{EAM}\)
Do đó: ΔADM=ΔAEM
Suy ra: AD=AE và MD=ME
Xet ΔDBM vuông tại D và ΔECM vuông tại E có
MB=MC
MD=ME
Do đó:ΔDBM=ΔECM
Suy ra: BD=EC
Ta có: AD+BD=AB
AE+EC=AC
mà AD=AE
và BD=CE
nên AB=AC
hay ΔABC cân tại A
cảm ơn bạn rất nhiều!!!
