DQ
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PQ
3
9 tháng 4 2016
bằng 39, đề thi violympic toán tỉnh mà bạn, thi vòng 9 là có
10 tháng 1 2019
trừ hai vế của PT cho 4 . ta được
\(\dfrac{x-291}{1700}-1+\dfrac{x-293}{1698}-1+\dfrac{x-295}{1696}-1+\dfrac{x-297}{1694}-1=4-4\)
<=> \(\dfrac{x-291-1700}{1700}+\dfrac{x-293-1698}{1698}+\dfrac{x-295-1696}{1696}+\dfrac{x-297-1694}{1694}=0\)
<=> \(\dfrac{x-1991}{1700}+\dfrac{x-1991}{1698}+\dfrac{x-1991}{1696}+\dfrac{x-1991}{1694}=0\)
<=> (x-1991)\(\left(\dfrac{1}{1700}+\dfrac{1}{1698}+\dfrac{1}{1696}+\dfrac{1}{1694}\right)=0\)
<=> x - 1991 = 0 ( vì \(\dfrac{1}{1700}+\dfrac{1}{1698}+\dfrac{1}{1696}+\dfrac{1}{1694}\)luôn lớn hơn 0 với mọi x)
<=> x = 1991
vậy x=1991
NT
1
9 tháng 6 2022
\(=\left(1+2-3-4\right)+\left(5+6-7-8\right)+...+\left(297+298-299-300\right)+301\)
\(=\left(-4\right)+\left(-4\right)+...+\left(-4\right)+301\)
\(=301-4\cdot75=301-300=1\)
22 tháng 4 2017
Giải
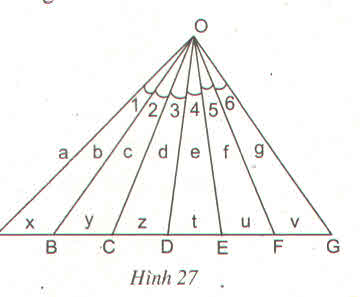
OB là tia phân giác trong của ∆OBC => xaxa = ycyc
OC là tia phân giác trong của ∆OBD => ydyd = zdzd
OD là tia phân giác trong của ∆OCE => zczc = tete
OE là tia phân giác trong của ∆ODF => tdtd = ufuf
OC là tia phân giác của ∆ACE => OCOAOCOA = CEOECEOE hay x+yax+ya = z+tez+te
OE là phân giác của ∆OCG => z+tcz+tc = u+vgu+vg
OD là phân giác của ∆AOG => x+y+xax+y+xa = t+u+vgt+u+vg
OD là phân giác của ∆OBF => y+zby+zb = t+uf
Y
20 tháng 7 2018
\(M=\dfrac{1}{337}.2\dfrac{1}{291}-\dfrac{290}{291}.\dfrac{1}{337}-\dfrac{2}{291.337}\)
\(M=\dfrac{1}{337}\left(2+\dfrac{1}{291}\right)-\left(1-\dfrac{1}{291}\right).\dfrac{1}{337}-2.\dfrac{1}{291.337}\)
Thay a = 1/337 ; b = 1/291 vào M, ta được
\(M=a\left(2+b\right)-\left(1-b\right)a-2ab\)
\(M=2a+ab-a+ab-2ab\)
\(M=a\)
\(M=\dfrac{1}{337}\)
366-363+360-357+354-351+…+300-297+294-291
=(366-363)+(360-357)+(354-351)+...+(300-297)+(294-291)
=3.13
=39
366-363+360-357+354-351+…+300-297+294-291
=(366-363)+(360-357)+(354-351)+...+(300-297)+(294-291)
=3.13
=39