Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Khi thay số âm vào mũ chẵn (2;4;6...) thì luôn luôn phải đóng mở ngoặc, nếu ko sẽ dẫn tới kết quả sai ngay lập tức:
Ví dụ: \(x^2-1\) với \(x=-2\)
Nếu đóng mở ngoặc: \(\left(-2\right)^2-1=3\) (đúng)
Không đóng mở ngoặc: \(-2^2-1=-5\) (sai)
Trong trường hợp mũ lẻ (mũ 1; 3; 5...) có thể không cần ngoặc nếu thấy đủ tự tin về khả năng toán của bản thân.

Chưa đúng đâu.
Ví dụ: \(\dfrac{1}{\sqrt[3]{x}-\sqrt[3]{y}}=\dfrac{\sqrt[3]{x^2}+\sqrt[3]{y^2}+\sqrt[3]{xy}}{x-y}\)
Tham khảo:
Trong toán học, đặc biệt là lý thuyết nhóm, các phần tử của một nhóm có thể được phân hoạch thành các lớp liên hợp; các phần tử của cùng một lớp liên hợp có nhiều tính chất chung, và việc nghiên cứu các lớp liên hợp của các nhóm không giao hoán cho ta biết nhiều đặc điểm quan trọng về cấu trúc của nhóm.[1][2] Trong mọi nhóm giao hoán, mọi lớp liên hợp đều là các tập chỉ chứa một phần tử.
Các hàm số nhận cùng một giá trị với các phần tử thuộc cùng một lớp liên hợp được gọi là các hàm lớp.

a)Trong toán học, đặc biệt là lý thuyết nhóm, các phần tử của một nhóm có thể được phân hoạch thành các lớp liên hợp; các phần tử của cùng một lớp liên hợp có nhiều tính chất chung, và việc nghiên cứu các lớp liên hợp của các nhóm không giao hoán cho ta biết nhiều đặc điểm quan trọng về cấu trúc của nhóm.
Ví dụ:
Xét một \(p-nhóm\) hữu hạn \(G\). Ta sẽ chứng minh rằng: mọi \(p-nhóm\) hữu hạn luôn có tâm không tầm thường.
Vì cấp của mọi lớp liên hợp của \(G\) phải chia hết cấp của \(G\) .Ta suy ra rằng mọi lớp liên hợp \(H_i\) có cấp \(p^{k_i}\) , với \(0< k_i< n\). Từ phương trình lớp ta suy ra:
Từ đây ta suy ra \(p\) là ước của \(|Z\left(G\right)|\), hay \(|Z\left(G\right)|\)\(>1\)
Tham khảo:
Trong toán học, đặc biệt là lý thuyết nhóm, các phần tử của một nhóm có thể được phân hoạch thành các lớp liên hợp; các phần tử của cùng một lớp liên hợp có nhiều tính chất chung, và việc nghiên cứu các lớp liên hợp của các nhóm không giao hoán cho ta biết nhiều đặc điểm quan trọng về cấu trúc của nhóm.
Ví dụ:
Xét một p−nhómp−nhóm hữu hạn GG. Ta sẽ chứng minh rằng: mọi p−nhómp−nhóm hữu hạn luôn có tâm không tầm thường.
Vì cấp của mọi lớp liên hợp của GG phải chia hết cấp của GG .Ta suy ra rằng mọi lớp liên hợp HiHi có cấp pkipki , với 0<ki<n0<ki<n. Từ phương trình lớp ta suy ra:

Từ đây ta suy ra pp là ước của |Z(G)||Z(G)|, hay |Z(G)||Z(G)|>1

bất đẳng thức cosi là khái niệm dùng để chỉ bất đẳng thức so sánh giữa trung bình cộng và trung bình nhân của n số thực không âm. Trong đó, trung bình cộng của n số thực không âm luôn lớn hơn hoặc bằng trung bình nhân của chúng
Hệ quả 1: Nếu tổng hai số dương không đổi thì tích của chúng lớn nhất khi hai số đó bằng nhau Hệ quả 2: Nếu tích hai số dương không đổi thì tổng của hai số này nhỏ nhất khi hai số đó bằng nhau

Tại sao không giải ra $\sqrt{P}$ và $\sqrt{P}$?
Em đã có $P$ rồi, nhưng với $\sqrt{P}$, em làm sao rút gọn được khi mà $P$ đã khá gọn rồi. Cũng chẳng có giá trị nào của $x$ để tính cụ thể $P, \sqrt{P}$ rồi đi so sánh. Vì vậy cách này không khả thi.
Vậy thì phải tìm hướng khác. Muốn so sánh 2 số, ta xét hiệu hai số đó.
$P-\sqrt{P}=\sqrt{P}(\sqrt{P}-1)$
Rõ ràng $\sqrt{P}$ đã dương rồi, giờ ta phải xem xét xem $\sqrt{P}-1$ âm hay dương, hay $P$ có lớn hơn 1 không
Đó là lý do vì sao bài giải như trên.
Còn câu hỏi khi nào giải ra từng cái $P$ và $\sqrt{P}$, thì đó là khi đề cho $x=2$ chả hạn, so sánh $P$ và $\sqrt{P}$.
Nhưg hầu như sẽ chẳng có đề nào ra kiểu vậy, mà đa số lợi dụng tính chất của phân thức đó để so sánh (ví dụ như trong bài tính chất nổi bật là $P>1$) cho nhanh. Đó là cái hay của đề bài.

dốc ngược tất cả số đĩa từ trục A( trên nhỏ dưới lớn) sang trục C(trên lớn dưới nhỏ) , xong lại tiếp tục dốc ngược qua trục B =]]
ahaha:D

Câu 1:
Giả sử giá niêm yết của cặp và giày lần lượt là $a$ và $b$ đồng
Theo bài ra ta có:
$a+b=850.000(1)$
$(a-15.000)+b(1-0,1)=785.000(2)$
Từ $(1);(2)\Rightarrow a=350.000$ (đồng) và $b=500.000$ (đồng)
Câu 2:
$x^3+y^3=(x+y)^3-3xy(x+y)=5^3-3(-2).5=155$
$x^2+y^2=(x+y)^2-2xy=5^2-2(-2)=29$
Khi đó:
$P=\frac{x^5+y^5}{x^2y^2}+2020=\frac{(x^3+y^3)(x^2+y^2)-x^2y^2(x+y)}{x^2y^2}+2020$
$=\frac{155.29-4.5}{4}+2020=3138,75$
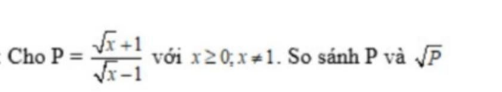
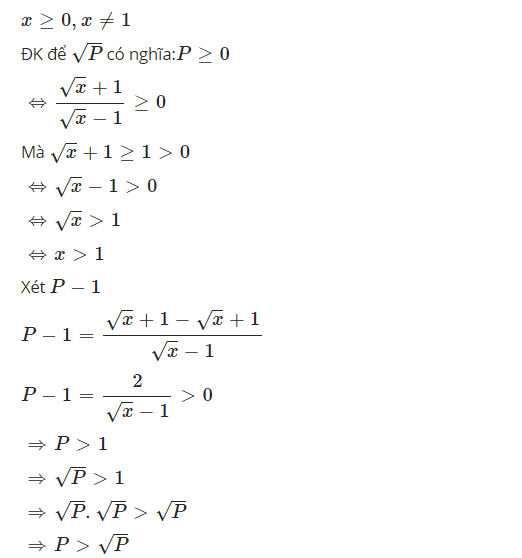
cái này mình không rõ nhưng cô mình bảo nên quy đồng bn nhé, chắc bởi trong chương trình thcs k có khái niệm nhân chéo
g