
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\frac{1}{2}.2^n+2^{2+n}=9.2^5\)
\(\frac{1}{2}.2^n+4.2^n=9.2^5\)
\(2^n.\left(\frac{1}{2}+4\right)=9.2^5\)
\(2^n.\frac{9}{2}=9.2^5\)
\(2^n=9.\frac{2}{9}.2^5\)
\(2^n=2.2^5\)
\(2^n=2^6\)
\(\Rightarrow n=6\)
\(\frac{1}{2}\)\(\times\)\(2^n\)\(+\)\(2^{2+n}\)\(=\)\(9\)\(\times\)\(2^5\)
\(\frac{1}{2}\)\(\times\)\(2^n\)\(\times\)\((\)\(1\)\(+\)\(2^2\)\()\)\(=\)\(9\)\(\times\)\(2^5\)
\(\frac{1}{2}\)\(\times\)\(2^n\)\(\times\)\(5\)\(=\)\(9\)\(\times\)\(2^5\)
\(2^n\)\(=\)\(9\)\(\times\)\(32\)\(\div\)\(5\)\(\times\)\(2\)
\(2^n\)\(=\)115,2


Số ki lô gam ông giảm sau tháng thứ nhất là : 100 : 100 x 10 = 10 ( kg )
Cân nặng của ông sau 1 tháng là : 100 - 10 = 90 ( kg )
Số ki lô gam ông giảm sau tháng thứ 2 là : 90 : 100 x 10= 9 ( kg )
Cân nặng của ông sau 2 tháng là : 90 - 9 = 81 ( kg )
Số ki lô gam ông giảm sau tháng thứ 3 là : 81 : 100 x 10 = 8,1 ( kg )
Cân nặng của ông sau 3 tháng là : 81 - 8,1 = 72,9 ( kg )
K nha mn !

=1(1+1) + 2(2+1) + 3(3+1) +...+n(n+1)
=(1^2 + 2^2 + 3^2 +...+ n^2) + (1 + 2 + 3 + ...+ n)
ta có các công thức:
1^2 + 2^2 + 3^2 +...+ n^2 = n(n+1)(2n+1)/6
1 + 2 + 3 + ...+ n = n(n+1)/2
thay vào ta có:
S = n(n+1)(2n+1)/6 + n(n+1)/2
=n(n+1)/2[(2n+1)/3 + 1]
=n(n+1)(n+2)/3

Ta có:\(B=\frac{3^6\times15^5+3^6\times15^6}{3^{10}\times5^5\times8}\)
\(B=\frac{3\times45^5+\left(3\times15\right)^6}{3^{10}\times5^5\times8}\)
\(B=\frac{\left(3+45\right)\times45^5}{3^{10}\times5^5\times8}\)
\(B=\frac{48\times15^5\times3^5}{3^{10}\times5^5\times8}\)
\(B=\frac{6\times3^5\times5^5}{3^5\times5^5}\)
\(B=6\)
Tớ làm hơi tắt nhé!

Theo đề ta có:
\(\dfrac{a}{\dfrac{1}{\dfrac{1}{2}}}=\dfrac{b}{\dfrac{1}{\dfrac{1}{5}}}=\dfrac{c}{\dfrac{1}{\dfrac{1}{7}}}\) và \(a+b-2c=70\)
Áp dụng tính chất của dãy tỉ số bằng nhay ta có:
\(\dfrac{a}{\dfrac{1}{\dfrac{1}{2}}}=\dfrac{b}{\dfrac{1}{\dfrac{1}{5}}}=\dfrac{c}{\dfrac{1}{\dfrac{1}{7}}}=\dfrac{a}{2}=\dfrac{b}{5}=\dfrac{c}{7}=\dfrac{2c}{2.7}=\dfrac{a+b-2c}{2+5-14}=\dfrac{70}{-7}=-10\)
\(\dfrac{a}{2}=-10\Rightarrow a=\left(-10\right).2=-20\)
\(\dfrac{b}{5}=-10\Rightarrow b=\left(-10\right).5=-50\)
\(\dfrac{c}{7}=-10\Rightarrow c=\left(-10\right).7=-70\)
Vậy \(a=-20;b=-50;c=-70\)

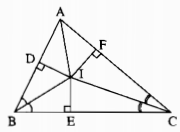
Kẻ: ID⊥AB,IE⊥BC,IF⊥ACID⊥AB,IE⊥BC,IF⊥AC
Xét hai tam giác vuông IDB và IEB, ta có:
\(\eqalign{
& \widehat {I{\rm{D}}B} = \widehat {IEB} = 90^\circ \cr
& \widehat {DBI} = \widehat {EBI}\left( {gt} \right) \cr} \)
BI cạnh huyền chung
⇒⇒ ∆IDB = ∆IEB (cạnh huyền, góc nhọn)
Suy ra: ID = IE (hai cạnh tương ứng)
Quảng cáo
Xét hai tam giác vuông IEC và IFC, ta có ;
\(\eqalign{
& \widehat {IEC} = \widehat {IFC} = 90^\circ \cr
& \widehat {ECI} = \widehat {FCI}\left( {gt} \right) \cr} \)
CI canh huyền chung
Suy ra: ∆ IEC = ∆IFC (cạnh huyền, góc nhọn)
Suy ra: IE = IF (hai cạnh tương ứng) (2)
Từ (1) và (2) suy ra: ID = IF
Xét hai tam giác vuông IDA và IFA, ta có:
ˆIDA=ˆIFA=90∘IDA^=IFA^=90∘
ID = IF (chứng minh trên)
AI cạnh huyền chung
Suy ra: ∆IDA = ∆IFA (cạnh huyền, cạnh góc vuông)
Suy ra: ˆDAI=ˆFAIDAI^=FAI^ (hai góc tương ứng)
Vậy AI là tia phân giác của ˆA
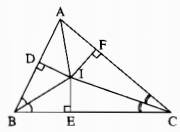
Kẻ: ID⊥AB,IE⊥BC,IF⊥ACID⊥AB,IE⊥BC,IF⊥AC
Xét hai tam giác vuông IDB và IEB, ta có:
ˆIDB=ˆIEB=90∘ˆDBI=ˆEBI(gt)IDB^=IEB^=90∘DBI^=EBI^(gt)
BI cạnh huyền chung
⇒⇒ ∆IDB = ∆IEB (cạnh huyền, góc nhọn)
Suy ra: ID = IE (hai cạnh tương ứng) (1)
Xét hai tam giác vuông IEC và IFC, ta có ;
ˆIEC=ˆIFC=90∘ˆECI=ˆFCI(gt)IEC^=IFC^=90∘ECI^=FCI^(gt)
CI canh huyền chung
Suy ra: ∆ IEC = ∆IFC (cạnh huyền, góc nhọn)
Suy ra: IE = IF (hai cạnh tương ứng) (2)
Từ (1) và (2) suy ra: ID = IF
Xét hai tam giác vuông IDA và IFA, ta có:
ˆIDA=ˆIFA=90∘IDA^=IFA^=90∘
ID = IF (chứng minh trên)
AI cạnh huyền chung
Suy ra: ∆IDA = ∆IFA (cạnh huyền, cạnh góc vuông)
Suy ra: ˆDAI=ˆFAIDAI^=FAI^ (hai góc tương ứng)
Vậy AI là tia phân giác của ˆA
Read more: https://sachbaitap.com/cau-100-trang-151-sach-bai-tap-sbt-toan-lop-7-tap-1-c7a10140.html#ixzz6DFwdbF2W

câu 2 Gọi số học sinh nam và nữ lần lượt là a , b (a,b>0)
vì số h/s nam và h/s nữ tỉ lệ với các số 5 và 7 nên: => a/5 = b/7
vì số học sinh nữ nhiều hơn nam là 6 nên: b-a=6
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
a/5=b/7=b-a/7-5=6/2=3
Do đó : a/5=3=>a=3x5=15(h/s)
b/7=3=>b=3x7=21(h/s)
Vậy số học sinh nam và nữ của lớp đó lần lượt là 15 h/s;21h/s
 2
2
Ta có : \(\frac{\left(-68\right)^6}{34^6}=\frac{68^6}{34^6}=\frac{34^6.2^6}{34^6}=2^6=64\)