N
3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
18 tháng 2 2020
\(u_n-1=\frac{2^n-5^n}{2^n+5^n}-1=\frac{-2.5^n}{2^n+5^n}\Rightarrow\frac{1}{u_n-1}=\frac{2^n+5^n}{-2.5^n}=-\frac{1}{2}\left(\left(\frac{2}{5}\right)^n+1\right)\)
\(\Rightarrow S_{10}=-\frac{1}{2}\left[\frac{2}{5}+\left(\frac{2}{5}\right)^2+...+\left(\frac{2}{5}\right)^{10}+10\right]\)
\(=-\frac{1}{2}\left[\frac{2}{5}.\frac{1-\left(\frac{2}{5}\right)^{10}}{1-\frac{2}{5}}+10\right]=\frac{1}{3}\left(\frac{2}{5}\right)^{10}-\frac{16}{3}\)
PT
1
TC
1
AH
Akai Haruma
Giáo viên
20 tháng 5 2020
Lời giải:
Trong các hàm kể trên có hàm số ở phương án A không xác định tại $x=-1$ nên hàm số đó gián đoạn tại điểm $x_0=-1$
Đáp án A.
NV
Nguyễn Việt Lâm
Giáo viên
2 tháng 1 2024
\(\lim\limits_{x\rightarrow1}f\left(x\right)=\lim\limits_{x\rightarrow1}\dfrac{x^3-x^2+2x-2}{x-1}=\lim\limits_{x\rightarrow1}\dfrac{x^2\left(x-1\right)+2\left(x-1\right)}{x-1}\)
\(=\lim\limits_{x\rightarrow1}\dfrac{\left(x-1\right)\left(x^2+2\right)}{x-1}=\lim\limits_{x\rightarrow1}\left(x^2+2\right)=3\)
\(f\left(1\right)=3.1+m=m+3\)
Hàm số liên tục tại \(x_0=1\) khi và chỉ khi \(\lim\limits_{x\rightarrow1}f\left(x\right)=f\left(1\right)\)
\(\Rightarrow m+3=3\Rightarrow m=0\)
14 tháng 5 2022
Bài 2:
a: \(=\dfrac{7}{9}\left(\dfrac{7}{6}-\dfrac{19}{20}-\dfrac{1}{15}\right)+\dfrac{22}{5}\cdot\dfrac{1}{24}\)
\(=\dfrac{7}{9}\cdot\dfrac{3}{20}+\dfrac{22}{120}=\dfrac{7}{60}+\dfrac{11}{60}=\dfrac{18}{60}=\dfrac{3}{10}\)
b: \(=\left(\dfrac{35-32}{60}\right)^2+\dfrac{4}{5}\cdot\dfrac{70-45}{80}\)
\(=\dfrac{1}{400}+\dfrac{4\cdot25}{400}=\dfrac{101}{400}\)
CM
23 tháng 12 2018
a. Δy = f(x0 + Δx) – f(x0) = f(1 + 1) – f(1) = f(2) – f(1) = 23 – 13 = 7
b. Δy = f(x0 + Δx) – f(x0) = f(1 – 0,1) – f(1) = f(0,9) – f(1) = (0,9)3 – 13 = -0,271.
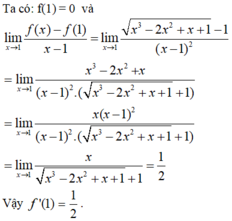
6 là kết quả của mk nha bn
Syntax ERROR
Ở đầu quên viết dấu "(" kìa
Nếu có dấu ")" ở đầu thì kết quả bằng 0