Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
(1) Nếu hàm số f(x) có đạo hàm tại điểm x = x 0 thì f(x) liên tục tại điểm đó. Đây là mệnh đề đúng.
(2) Nếu hàm số f (x) liên tục tại điểm x = x 0 thì f(x) có đạo hàm tại điểm đó.
Phản ví dụ
Lấy hàm f ( x ) = x ta có D= R nên hàm số f(x) liên tục trên R.
Nhưng ta có l i m x → 0 + f ( x ) - f ( 0 ) x - 0 = l i m x → 0 + x - 0 x - 0 = l i m x → 0 + x - 0 x - 0 = 1 l i m x → 0 - f ( x ) - f ( 0 ) x - 0 = l i m x → 0 - x - 0 x - 0 = l i m x → 0 - - x - 0 x - 0 = - 1
Nên hàm số không có đạo hàm tại x = 0.
Vậy mệnh đề (2) là mệnh đề sai.
(3) Nếu f(x) gián đoạn tại x = x 0 thì chắc chắn f(x) không có đạo hàm tại điểm đó.
Vì (1) là mệnh đề đúng nên ta có f(x) không liên tục tại x = x 0 thì f(x) không có đạo hàm tại điểm đó.
Vậy (3) là mệnh đề đúng.

+) (1) Nếu hàm số f(x) có đạo hàm tại điểm Xét ba mệnh đề sau:
(1) Nếu hàm số f(x) có đạo hàm tại điểm x = x 0 thì f(x) liên tục tại điểm đó.
(2) Nếu hàm số f(x) liên tục tại điểm x = x 0 thì f(x) có đạo hàm tại điểm đó.
- Trong ba câu trên: thì f(x) liên tục tại điểm đó. Đây là mệnh đề đúng.
+) (2) Nếu hàm số f(x) liên tục tại điểm x = x 0 thì f(x) có đạo hàm tại điểm đó.Đây là mệnh đề sai.
Phản ví dụ:
- Lấy hàm f(x) = |x| ta có D = R nên hàm số f(x) liên tục trên R
- Nhưng ta có
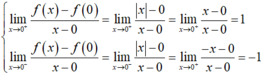
- Nên hàm số không có đạo hàm tại x = 0.
- Vậy mệnh đề (2) là mệnh đề sai.
+) (3) Nếu f(x) gián đoạn tại x = x 0 thì chắc chắn f(x) không có đạo hàm tại điểm đó.
- Vậy (3) là mệnh đề đúng.Vì (1) là mệnh đề đúng nên ta có f(x) không liên tục tại x = x 0 thì f(x) không có đạo hàm tại điểm đó.
- Vậy (3) là mệnh đề đúng.
Chọn A.

+) (1) Nếu hàm số f(x) có đạo hàm tại điểm Xét ba mệnh đề sau:
(1) Nếu hàm số f(x) có đạo hàm tại điểm x = x 0 thì f(x) liên tục tại điểm đó.
(2) Nếu hàm số f(x) liên tục tại điểm x = x 0 thì f(x) có đạo hàm tại điểm đó.
- Trong ba câu trên: thì f(x) liên tục tại điểm đó. Đây là mệnh đề đúng.
+) (2) Nếu hàm số f(x) liên tục tại điểm x = x 0 thì f(x) có đạo hàm tại điểm đó.Đây là mệnh đề sai.
Phản ví dụ:
- Lấy hàm f(x) = |x| ta có D = R nên hàm số f(x) liên tục trên R
- Nhưng ta có
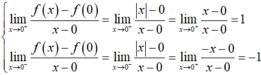
- Nên hàm số không có đạo hàm tại x = 0.
- Vậy mệnh đề (2) là mệnh đề sai.
+) (3) Nếu f(x) gián đoạn tại x = x 0 thì chắc chắn f(x) không có đạo hàm tại điểm đó.
- Vậy (3) là mệnh đề đúng.Vì (1) là mệnh đề đúng nên ta có f(x) không liên tục tại x = x 0 thì f(x) không có đạo hàm tại điểm đó.
- Vậy (3) là mệnh đề đúng.
Chọn A.

(1) Nếu hàm số f(x) có đạo hàm tại điểm x = x 0 thì f(x) liên tục tại điểm đó. Đây là mệnh đề đúng.
(2) Nếu hàm số f(x) liên tục tại điểm x = x 0 thì f(x) có đạo hàm tại điểm đó. Đây là mệnh đề sai.
+)Với mọi
x
0
≠ 0 thì 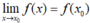
+)Lại có:
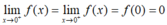
→ Nên hàm số f(x) liên tục trên R.
+) Nhưng ta có:
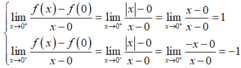
→ Nên hàm số không có đạo hàm tại x = 0.
→ Vậy mệnh đề (2) là mệnh đề sai.
(3) Nếu f(x) gián đoạn tại x = x 0 thì chắc chắn f(x) không có đạo hàm tại điểm đó.
- Vì (1) là mệnh đề đúng nên ta suy ra : Nếu f(x) không liên tục tại x = x 0 thì f(x) không có đạo hàm tại điểm đó.
- Vậy (3) là mệnh đề đúng.
Chọn A.

b) \(3\left(1-2x\right)^{20}\left(3x-2\right)^{10}\left(-14\left(3x-2\right)+11\left(1-2x\right)\right)\)

Chọn A.
Với x = 1 ta có f(1) = k2
Với x ≠ 1 ta có
![]()
suy ra ![]() .
.
Vậy để hàm số gián đoạn tại x = 1 khi ![]() ⇔ k2 ≠ 4 ⇔ k ≠ ±2.
⇔ k2 ≠ 4 ⇔ k ≠ ±2.

- TXĐ: D = R.
+ Với x = 1 ta có f ( 1 ) = k 2
+ Với x ≠ 1 ta có:
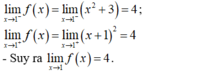
- Vậy để hàm số gián đoạn tại x = 1 khi và chỉ khi:
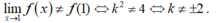
Chọn A

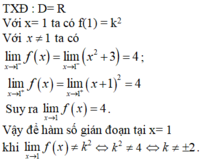
Lời giải:
Trong các hàm kể trên có hàm số ở phương án A không xác định tại $x=-1$ nên hàm số đó gián đoạn tại điểm $x_0=-1$
Đáp án A.