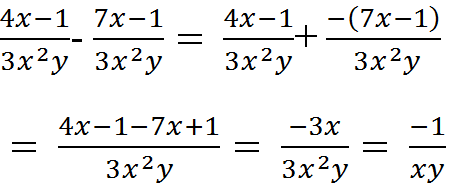ML
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
15 tháng 11 2017
Bài 1: Ta có: \(B=\dfrac{4+2\left|4-2x\right|}{5}\)
Do \(\left|4-2x\right|\ge0\left(\forall x\right)\Rightarrow2\left|4-2x\right|\ge0\left(\forall x\right)\)
Dấu "=" xảy ra \(\Leftrightarrow\left|4-2x\right|=0\Leftrightarrow x=2\)
\(\Rightarrow MinB=\dfrac{4+2.0}{5}=\dfrac{4}{5}\)
Vậy GTNN của \(B=\dfrac{4}{5}\Leftrightarrow x=2\)
Bài 2:a, \(A=\dfrac{12}{3+\left|5x+1\right|+\left|2y-1\right|}\)
Do \(\left|5x+1\right|\ge0\left(\forall x\right);\left|2y-1\right|\ge0\left(\forall y\right)\)
Dấu "=" xảy ra \(\Leftrightarrow x=-\dfrac{1}{5};y=\dfrac{1}{2}\)
\(\Rightarrow\left|5x+1\right|+\left|2y-1\right|\ge0\left(\forall x;y\right)\)
\(\Rightarrow3+\left|5x+1\right|+\left|2y-1\right|\ge3\left(\forall x;y\right)\)
\(\Rightarrow\dfrac{1}{3+\left|5x+1\right|+\left|2y-1\right|}\le\dfrac{1}{3}\left(\forall x;y\right)\)
\(\Rightarrow A=\dfrac{12}{3+\left|5x+1\right|+\left|2y-1\right|}\le4\left(\forall x;y\right)\)
Vậy Max A = 4 \(\Leftrightarrow x=-\dfrac{1}{5};y=\dfrac{1}{2}\)
b, \(B=\dfrac{5}{\left(4x^2+4x+1\right)+\left(y^2+2y+1\right)+1}=\dfrac{5}{\left(2x+1\right)^2+\left(y+1\right)^2+1}\)Bn tự cm: \(\left(2x+1\right)^2+\left(y+1\right)^2+1\ge1\left(\forall x;y\right)\)
Dấu "=" xảy ra \(\Leftrightarrow x=-\dfrac{1}{2};y=-1\)
Vậy ta cx dễ dàng tìm được: Max\(B=\dfrac{5}{0+0+1}=5\) \(\Leftrightarrow x=-\dfrac{1}{2};y=-1\)
15 tháng 4 2018
a)
\(A=\dfrac{2x^2-16x+41}{x^2-8x+22}=\dfrac{2\left(x^2-8x+22\right)-3}{x^2-8x+22}\)
\(A-2=-\dfrac{3}{x^2-8x+22}=-\dfrac{3}{\left(x-4\right)^2+6}\ge-\dfrac{3}{6}=-\dfrac{1}{2}\)
\(A\ge\dfrac{3}{2}\) khi x =4
EC
0
14 tháng 10 2017
a,
\(x^2+4x+6=x^2+4x+4+2=\left(x+2\right)^2+2\ge2\)
\(=>A=\dfrac{x^2+4x+6}{3}\ge\dfrac{2}{3}\)
Vậy giá trị nhỏ nhất của biểu thức là 2/3 , dấu ''='' xảy ra khi và chỉ khi x = -2 .
b, \(Ta,c\text{ó}:\left|1-2x\right|\ge0\)
\(=>4+\left|1-2x\right|\ge4\)
\(=>\dfrac{4+\left|1+2x\right|}{5}\ge\dfrac{4}{5}\)
Vậy giá trị nhỏ nhất của biểu thức là 4/5 , dấu bằng xảy ra khi và chỉ khi 1 - 2x = 0 => x = 1/2
c,
\(\dfrac{5}{4x^2+4x+2y+y^2+3}\)
\(=\dfrac{5}{\left(2x+1\right)^2+\left(y+1\right)^2+1}\ge\dfrac{5}{1}=5\)
Vậy giá trị nhỏ nhất của biểu thức là 5 , dấu '='' xảy ra khi và chỉ khi
\(\left\{{}\begin{matrix}2x+1=0\\y+1=0\end{matrix}\right.< =>\left\{{}\begin{matrix}x=-\dfrac{1}{2}\\y=-1\end{matrix}\right.\)
DT
1
26 tháng 8 2017
\(K=\dfrac{3-4x}{x^2+1}\)
\(\Leftrightarrow Kx^2+1=3-4x\)
\(\Leftrightarrow Kx^2+4x+K-3=0\)
Để phương thức trên tồn tại \(x\) thì:
\(\text{4-K.(K-3)=K^2}+3K+4\ge0\)
\(\Leftrightarrow K^2-3.K-4\le0\)
\(\Leftrightarrow\left(K+1\right).\left(K-4\right)\le0\)
\(\Leftrightarrow-1\le K\le4\)
Vậy \(MIN\left(K\right)=-1\)
\(MAX\left(K\right)=4\)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
19 tháng 8 2024
B = 2\(x^2\) - 4\(x\) - 8
B = 2(\(x^2\) - 2\(x\) + 4) - 16
B = 2(\(x-2\))2 - 16
Vì (\(x-2\))2 ≥ 0 ∀ \(x\) ⇒ 2(\(x-2\))2 ≥ 0 ∀ \(x\)
⇒ 2(\(x-2\))2 - 16 ≥ -16 ∀ \(x\)
Dấu bằng xảy ra khi (\(x-2\))2 = 0 ⇒ \(x-2=0\) ⇒ \(x=2\)
Vậy Bmin = -16 khi \(x=2\)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
19 tháng 8 2024
Tìm min của C biết:
C = \(x^2\) - 2\(xy\) + 2y2 + 2\(x\) - 10y + 17
C = (\(x^2\) - 2\(xy\) + y2) + 2(\(x\) - y) + y2 - 8y + 16 + 1
C = (\(x\) - y)2 + 2(\(x\) - y) + 1 + (y2 - 8y + 16)
C = (\(x-y+1\))2 + (y - 4)2
Vì (\(x\) - y + 1)2 ≥ 0 ∀ \(x;y\); (y - 4)2 ≥ 0 ∀ y
Dấu bằng xảy ra khi: \(\left\{{}\begin{matrix}x-y+1=0\\y-4=0\end{matrix}\right.\) ⇒ \(\left\{{}\begin{matrix}x-y+1=0\\y=4\end{matrix}\right.\)
⇒ \(\left\{{}\begin{matrix}x-4+1=0\\y=4\end{matrix}\right.\) ⇒ \(\left\{{}\begin{matrix}x=-1+4\\y=4\end{matrix}\right.\) ⇒ \(\left\{{}\begin{matrix}x=3\\y=4\end{matrix}\right.\)
Vậy Cmin = 0 khi (\(x;y\)) = (3; 4)
NN
29 tháng 11 2017
a) \(\dfrac{4x-1}{3x^2y}-\dfrac{7x-1}{3x^2y}\)
\(=\dfrac{\left(4x-1\right)-\left(7x-1\right)}{3x^2y}\)
\(=\dfrac{4x-1-7x+1}{3x^2y}\)
\(=\dfrac{-3x}{3x^2y}\)
\(=\dfrac{-1}{xy}\)
b) \(\dfrac{4x+5}{2x-1}-\dfrac{5-9x}{2x-1}\)
\(=\dfrac{\left(4x+5\right)-\left(5-9x\right)}{2x-1}\)
\(=\dfrac{4x+5-5+9x}{2x-1}\)
\(=\dfrac{13x}{2x-1}\)
c) \(\dfrac{11x}{2x-3}-\dfrac{x-18}{3-2x}\)
\(=\dfrac{11x}{2x-3}+\dfrac{x-18}{2x-3}\)
\(=\dfrac{11x+\left(x-18\right)}{2x-3}\)
\(=\dfrac{11x+x-18}{2x-3}\)
\(=\dfrac{12x-18}{2x-3}\)
\(=\dfrac{6\left(2x-3\right)}{2x-3}\)
\(=\dfrac{6}{1}\)
\(=6\)
d) \(\dfrac{2x-7}{10x-4}-\dfrac{3x+5}{4-10x}\)
\(=\dfrac{2x-7}{10x-4}+\dfrac{3x+5}{10x-4}\)
\(=\dfrac{\left(2x-7\right)+\left(3x+5\right)}{10x-4}\)
\(=\dfrac{2x-7+3x+5}{10x-4}\)
\(=\dfrac{5x-2}{10x-4}\)
\(=\dfrac{5x-2}{2\left(5x-2\right)}\)
\(=\dfrac{1}{2}\)
MD
1
3 tháng 4 2018
Mình giải phương pháp tìm miền giá trị
\(A=\dfrac{4x+3}{x^2+1}\)
\(\Leftrightarrow Ax^2-4x+A-3=0\)(1)
+)Xét A=0\(\Rightarrow-4x-3=0\Leftrightarrow x=-\dfrac{3}{4}\)
+)Xét \(A\ne0\)
=>Để pt(1) có nghiệm thì \(\Delta=16-4A\left(A-3\right)\ge0\)
\(\Leftrightarrow4-A\left(A-3\right)\ge0\)
\(\Leftrightarrow-A^2+3A+4\ge0\)
\(\Leftrightarrow\left(A-4\right)\left(-A-1\right)\ge0\)
\(\Leftrightarrow-1\le A\le4\)
Vậy \(MINA=-1\Leftrightarrow\)x=-2
\(MAX=4\Leftrightarrow x=\)\(\dfrac{1}{2}\)