Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1.
\(G=\dfrac{2}{x^2+8}\le\dfrac{2}{8}=\dfrac{1}{4}\)
\(G_{max}=\dfrac{1}{4}\) khi \(x=0\)
\(H=\dfrac{-3}{x^2-5x+1}\) biểu thức này ko có min max
2.
\(D=\dfrac{2x^2-16x+41}{x^2-8x+22}=\dfrac{2\left(x^2-8x+22\right)-3}{x^2-8x+22}=2-\dfrac{3}{\left(x-4\right)^2+6}\ge2-\dfrac{3}{6}=\dfrac{3}{2}\)
\(D_{min}=\dfrac{3}{2}\) khi \(x=4\)
\(E=\dfrac{4x^4-x^2-1}{\left(x^2+1\right)^2}=\dfrac{-\left(x^4+2x^2+1\right)+5x^4+x^2}{\left(x^2+1\right)^2}=-1+\dfrac{5x^4+x^2}{\left(x^2+1\right)^2}\ge-1\)
\(E_{min}=-1\) khi \(x=0\)
\(G=\dfrac{3\left(x^2-4x+5\right)-5}{x^2-4x+5}=3-\dfrac{5}{\left(x-2\right)^2+1}\ge3-\dfrac{5}{1}=-2\)
\(G_{min}=-2\) khi \(x=2\)

Ta có : \(P=2x^2-8x+1=2\left(x^2-4x\right)+1=2\left(x^2-4x+4-4\right)+1=2\left(x-2\right)^2-7\)
Vì \(2\left(x-2\right)^2\ge0\forall x\)
Nên : \(P=2\left(x-2\right)^2-7\ge-7\forall x\in R\)
Vậy \(P_{min}=-7\) khi x = 2

\(b,Q=-5x^2-4x+1\)
\(=-5\left(x^2+\dfrac{4}{5}x+\dfrac{4}{25}\right)+\dfrac{9}{5}\)
\(=-5\left(x+\dfrac{2}{5}\right)^2+\dfrac{9}{5}\)
Với mọi giá trị của x ta có:
\(-5\left(x+\dfrac{2}{5}\right)^2\le0\)
\(\Rightarrow-5\left(x+\dfrac{2}{5}\right)^2+\dfrac{9}{5}\le\dfrac{9}{5}\)
Vậy MaxQ = \(\dfrac{9}{5}\)
Để Q = \(\dfrac{9}{5}\) thì \(x+\dfrac{2}{5}=0\Rightarrow x=-\dfrac{2}{5}\)
\(c,K=x\left(x-3\right)\left(x-4\right)\left(x-7\right)\)
\(=x\left(x-7\right)\left(x-3\right)\left(x-4\right)\)
\(=\left(x^2-7x\right)\left(x^2-7x+12\right)\)
Đặt \(x^2-7x+6=t\) , ta có:
\(K=\left(t-6\right)\left(t+6\right)\)
\(=t^2-36\)
\(=\left(x^2-7x+6\right)^2-36\)
Với mọi giá trị của x ta có:
\(\left(x^2-7x+6\right)^2\ge0\Rightarrow\left(x^2-7x+6\right)^2-36\ge-36\)
Vậy Min K = -36
Để K = - 36 thì \(x^2-7x+6=0\)
\(\Leftrightarrow x^2-x-6x+6=0\)
\(\Leftrightarrow x\left(x-1\right)-6\left(x-1\right)=0\)
\(\Leftrightarrow\left(x-6\right)\left(x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-6=0\\x-1=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=6\\x=1\end{matrix}\right.\)
a)\(P=2x^2-8x+1\)
=\(2\left(x^2-4x+4\right)-7\)
=\(2\left(x-2\right)^2-7\)
Với mọi x thì \(2\left(x-2\right)^2>=0\)
=>\(2\left(x-2\right)^2-7>=-7\)
Hay \(P>=-7\) với mọi x
Để \(P=-7\) thì
\(\left(x-2\right)^2=0\)
=>\(x-2=0\)
=>\(x=2\)
Vậy...
Các câu sau tương tự

`a,ĐKXĐ:x-4 ne 0,2x+2 ne 0`
`<=>x ne 4,x me -1`
`b,ĐKXĐ:4x^2-25 ne 0`
`<=>(2x-5)(2x+5) ne 0`
`<=>x ne +-5/2`
`c,ĐKXĐ:8x^3+27 ne 0`
`<=>8x^3 ne -27`
`<=>2x ne -3`
`<=>x ne -3/2`
`d,2x+2 ne 0,4y^2-9 ne 0`
`<=>2x ne -2,(2y-3)(2y+3) ne 0`
`<=>x ne -1,y ne +-3/2`
b) ĐKXĐ: \(x\notin\left\{\dfrac{5}{2};-\dfrac{5}{2}\right\}\)
c) ĐKXĐ: \(x\ne-\dfrac{3}{2}\)
d) ĐKXĐ: \(\left\{{}\begin{matrix}x\ne-1\\y\notin\left\{\dfrac{3}{2};-\dfrac{3}{2}\right\}\end{matrix}\right.\)

Tìm min:
$F=3x^2+x-2=3(x^2+\frac{x}{3})-2$
$=3[x^2+\frac{x}{3}+(\frac{1}{6})^2]-\frac{25}{12}$
$=3(x+\frac{1}{6})^2-\frac{25}{12}\geq \frac{-25}{12}$
Vậy $F_{\min}=\frac{-25}{12}$. Giá trị này đạt tại $x+\frac{1}{6}=0$
$\Leftrightarrow x=\frac{-1}{6}$
Tìm min
$G=4x^2+2x-1=(2x)^2+2.2x.\frac{1}{2}+(\frac{1}{2})^2-\frac{5}{4}$
$=(2x+\frac{1}{2})^2-\frac{5}{4}\geq 0-\frac{5}{4}=\frac{-5}{4}$ (do $(2x+\frac{1}{2})^2\geq 0$ với mọi $x$)
Vậy $G_{\min}=\frac{-5}{4}$. Giá trị này đạt tại $2x+\frac{1}{2}=0$
$\Leftrightarrow x=\frac{-1}{4}$

\(a,=\dfrac{x^2+4x+3-2x^2+2x+x^2-4x+3}{\left(x-3\right)\left(x+3\right)}=\dfrac{2\left(x+3\right)}{\left(x-3\right)\left(x+3\right)}=\dfrac{2}{x-3}\\ b,=\dfrac{1-2x+3+2y+2x-4}{6x^3y}=\dfrac{2y}{6x^3y}=\dfrac{1}{x^2}\\ c,=\dfrac{75y^2+18xy+10x^2}{30x^2y^3}\\ d,=\dfrac{5x+8-x}{4x\left(x+2\right)}=\dfrac{4\left(x+2\right)}{4x\left(x+2\right)}=\dfrac{1}{x}\\ c,=\dfrac{x^2+2+2x-2-x^2-x-1}{\left(x-1\right)\left(x^2+x+1\right)}=\dfrac{x-1}{\left(x-1\right)\left(x^2+x+1\right)}=\dfrac{1}{x^2+x+1}\)
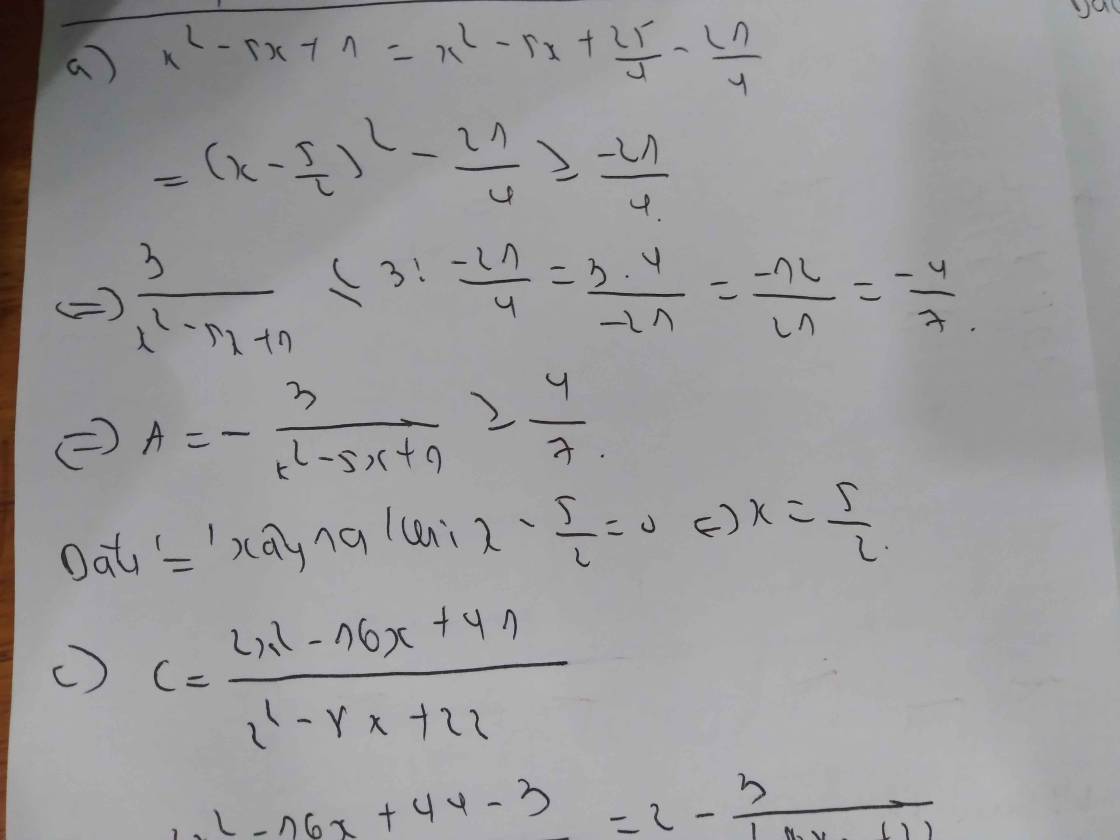
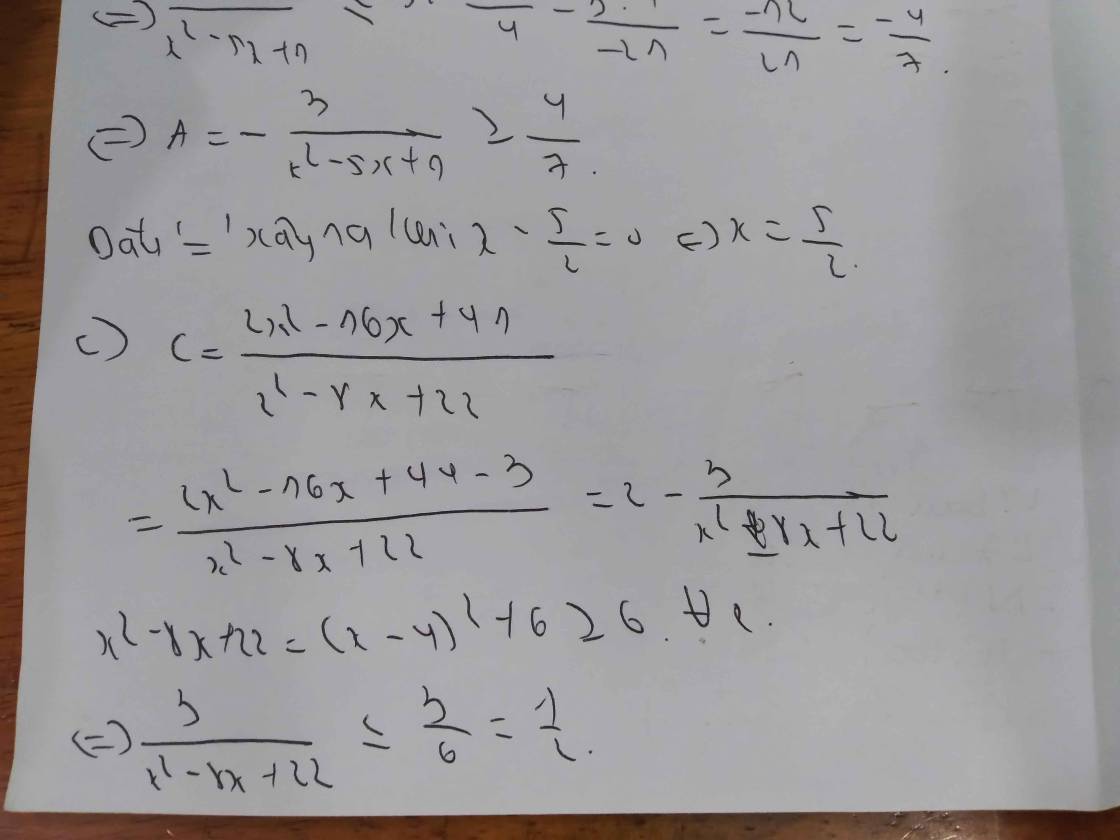
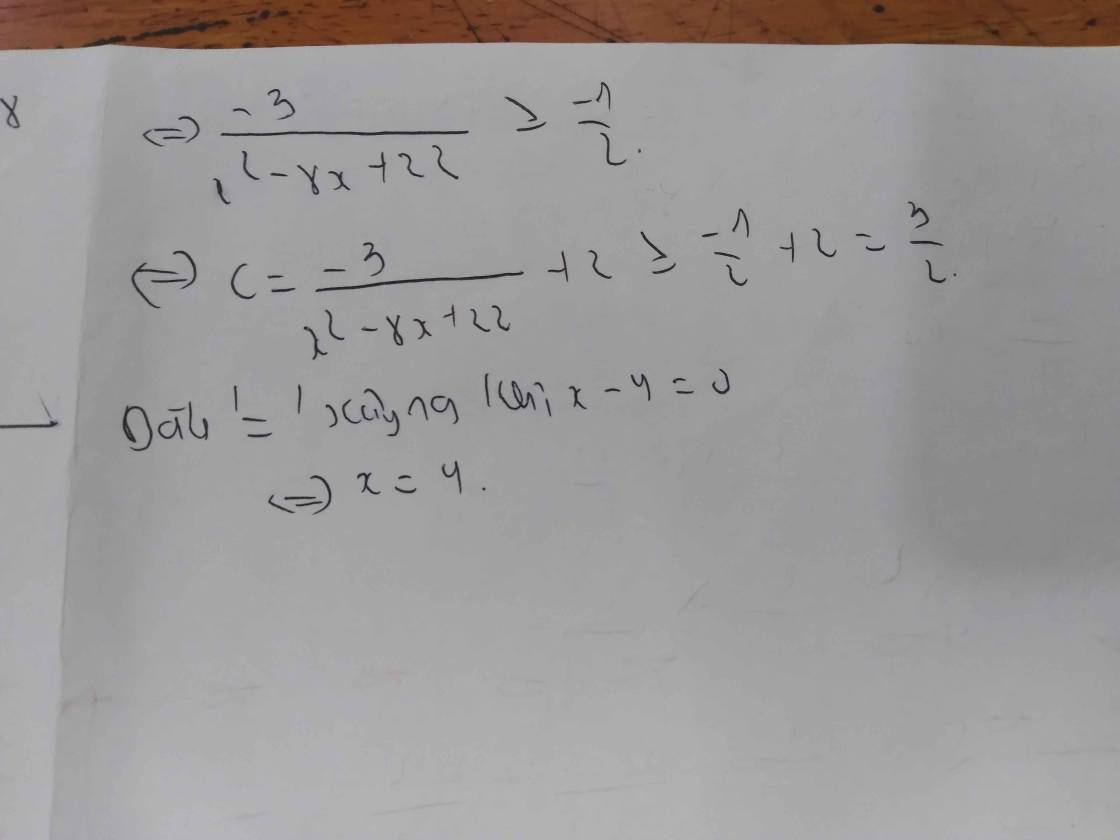
a)
\(A=\dfrac{2x^2-16x+41}{x^2-8x+22}=\dfrac{2\left(x^2-8x+22\right)-3}{x^2-8x+22}\)
\(A-2=-\dfrac{3}{x^2-8x+22}=-\dfrac{3}{\left(x-4\right)^2+6}\ge-\dfrac{3}{6}=-\dfrac{1}{2}\)
\(A\ge\dfrac{3}{2}\) khi x =4