K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
LT
3
ST
22 tháng 11 2018
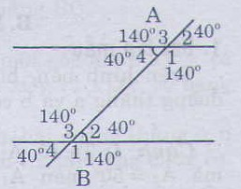
Xét ΔDAEΔDAE và ΔBOCΔBOC có:
+) AD=OB(=r)AD=OB(=r)
+) DE=BCDE=BC (gt)
+) AE=OC(=r)AE=OC(=r)
Suy ra ΔDAE=ΔBOC(c.c.c)∆DAE=∆BOC(c.c.c)
Suy ra ˆDAE=ˆBOCDAE^=BOC^ (hai góc tương tứng)
Mà ˆBOC=ˆxOy.BOC^=xOy^.
Do đó: ˆDAE=ˆxOy.DAE^=xOy^. (điều phải chứng minh)
TT
1
HP
14 tháng 9 2015
bài 36: 108 . 28 = (10 . 2)8 = 208
108 : 28 = (10 : 2)8 = 58
254 . 28 = (52)4 . 28 = 58 . 28 = (5 . 2)8 = 108
158 . 94 = 158 . (32)4 = 158 . 38 = (15 . 3)8 = 458
272 : 253 = (33)2 : (52)3 = 36 : 56 = \(\left(\frac{3}{5}\right)^6\)
bài 37: \(\frac{4^2.4^3}{2^{10}}=\frac{4^5}{2^{10}}=\frac{\left(2^2\right)^5}{2^{10}}=\frac{2^{10}}{2^{10}}=1\)
\(\frac{\left(0,6\right)^5}{\left(0,2\right)^6}=\frac{\left(0,2.3\right)^5}{\left(0,2\right)^6}=\frac{\left(0,2\right)^5.3^5}{\left(0,2\right)^6}=\frac{3^5}{0,2}=1215\)
\(\frac{2^7.9^3}{6^5.8^2}=\frac{2^7.\left(3^2\right)^3}{\left(2.3\right)^5.\left(2^3\right)^2}=\frac{2^7.3^6}{2^5.3^5.2^6}=\frac{2^7.3}{2^{11}}=\frac{3}{2^4}=\frac{3}{16}\)
\(\frac{6^3+3.6^2+3^3}{-13}=\frac{\left(2.3\right)^3+3.\left[\left(2.3\right)^2\right]+3^3}{-13}=\frac{2^3.3^3+3.2^2.3^2+3^3}{-13}=\frac{3^3.\left(2^3+2^2+1\right)}{-13}=\frac{3^3.13}{-13}\) = -33 = -27
MH
30 tháng 7 2017
a) Viết các số \(2^{27}\) và \(3^{18}\) dưới dạng các lũy thừa có số mũ là 9
b) Trong hai số \(2^{27}\) và \(3^{18}\), số nào lớn hơn?
Giải :
a) Ta có: \(2^{27}\)= \(\left(2^3\right)^9\) = \(8^9\)
318 = \(\left(3^2\right)^9\) = \(9^9\)
b) Theo kq câu a ,ta có :
\(2^{27}\) = \(8^9\) ; \(3^{18}\)= \(9^9\)
Vì 8 < 9 => \(8^9\)< \(9^9\)
Vậy \(2^{27}\) < \(3^{18}\)