Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

k đúng đâu cô giáo mk bảo x là đẳng thức,phải giải chi tiết ra

a ) Khi \(f\left(2\right)\)
\(5.2+1-\left|5.2-3\right|\)
\(=10+1-\left|10-3\right|\)
\(=10+1-7\)
\(=4\)
Khi \(f\left(-7\right)\)
\(5.\left(-7\right)+1-\left|2.\left(-7\right)-3\right|\)
\(=-35+1-\left|-14-3\right|\)
\(=-34-\left|-17\right|\)
\(=-34-17\)
\(=-51\)
b ) Khi \(f\left(2\right)\) , thì :
\(5.2+1-2.2-3\)
\(=10+1-4-3\)
\(=4\)
Khi \(f\left(-7\right)\) , thì :
\(5.\left(-7\right)+1-2.\left(-7\right)-3\)
\(=-35+1+14-3\)
.\(=-23\)

Vẽ đồ thị giùm nha! Giúp câu chứng minh thôi. Ở đây vẽ đồ thị xấu lém =,=
Ta có: \(y=f\left(x\right)=3x^2+5\)
Ta có: \(x^2\ge0\forall x\) (luôn đúng)
Nên \(3x^2\ge0\). do đó \(y=f\left(x\right)=3x^2+5\ge5\forall x\)
Vậy hàm số \(y=f\left(x\right)=3x^2+5\) luôn dương với mọi x. (đpcm)

Bài 2:
\(3x^2+5\ge5>0\forall x\)
nên f(x)>0 với mọi x

Với mọi \(x\in R\) , ta có \(3x^2\ge0\) suy ra \(3x^2+5>5\). Vì vậy với mọi giá trị x thì hàm số đã cho nhận giá trị dương.

a) Thay x=-9 vào hàm số y=f(x)=\(\frac{2}{3}\)x+6 ta có :
y=f(x)=\(\frac{2}{3}\).(-9)+6=0
Thay x=12 vào hàm số y=f(x)=\(\frac{2}{3}x+6\) ta có :
y=f(x)=\(\frac{2}{3}\).12+6 = 14
b) + Ta có : \(\frac{2}{3}x+6=5\)
2/3x=5-6
2/3x=-1
=> x=-3/2
+ Ta có : 2/3x+6=-4
2/3x=(-4)-6
2/3x=-10
=>x=-15
c) Giá trị của y lần lượt ={4,16/3,-6,8,26/3,10}
d) y=0 <=> 2/3x+6=0
2/3x=-6
=>x=-9

Điền giá trị y = f(x) vào bảng sau:
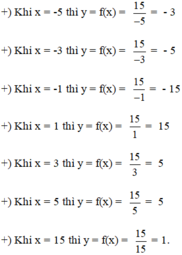
| x | -5 | -3 | -1 | 1 | 3 | 5 | 15 |
| y=f(x) | -3 | -5 | -15 | 15 | 5 | 3 | 1 |

ta có hàm số y = f(x) = 3x2 + 5
vì x2 \(\ge\)0 \(\forall\)x \(\Rightarrow\)3x2 + 5 \(\ge\)5 hay y \(\ge\)5
Vậy với mọi giá trị của x thì hàm số đã cho luôn nhận giá trị dương
Vì x2>0 ( với mọi x ) nên 3x2+5 > 0
Vậy f(x) = 3x2 + 5 luôn nhận giá trị dương với mọi giá trị x ( đpcm ).
XONG RỒI ĐÓ...