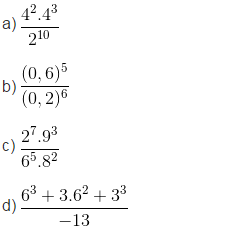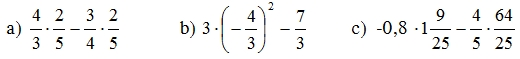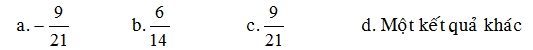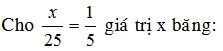K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
so sánh các số hữu tỉ
LB
22 tháng 5 2019
VD1: So sánh hai số hữu tỉ -0,6 và 1−21−2
Giải:
Ta có: −0,6=−610;1−2=−510.−0,6=−610;1−2=−510.
Vì −6<−5−6<−5 và 10>010>0 nên −610<−510−610<−510 hay −0,6<1−2−0,6<1−2 .
- Nếu x > y thì trên trục số, điểm x ở bên trái điểm y.
- Số hữu tỉ lớn hơn 0 gọi là số hữu tỉ dương;
Số hữu tỉ nhỏ hơn 0 gọi là số hữu tỉ âm;
Số hữu tỉ 0 không là số hữu tỉ dương cũng không là số hữu tỉ âm.
6 tháng 9 2017
a,
\(\left(\dfrac{-2}{3}+\dfrac{3}{7}\right):\dfrac{4}{5}+\left(-\dfrac{1}{3}+\dfrac{4}{7}\right):\dfrac{4}{5}\)
\(=\left(\dfrac{-2}{3}+\dfrac{-1}{3}+\dfrac{3}{7}+\dfrac{4}{7}\right):\dfrac{4}{5}\)
\(=\left(-1+1\right):\dfrac{4}{5}=0\)
b,
PA
5 tháng 7 2016
a.
\(\frac{4^2\times4^3}{2^{10}}=\frac{4^2\times4^3}{2^{2\times5}}=\frac{4^2\times4^3}{\left(2^2\right)^5}=\frac{4^5}{4^5}=1\)
b.
\(\frac{\left(0,6\right)^5}{\left(0,2\right)^6}=\frac{\left(0,2\times3\right)^5}{\left(0,2\right)^6}=\frac{\left(0,2\right)^5\times3^5}{\left(0,2\right)^6}=\frac{243}{0,2}=1215\)
c.
\(\frac{2^7\times9^3}{6^5\times8^2}=\frac{2^7\times\left(3^2\right)^3}{\left(2\times3\right)^5\times\left(2^3\right)^2}=\frac{2^7\times3^6}{2^5\times3^5\times2^6}=\frac{3}{2^4}=\frac{3}{16}\)
d.
\(\frac{6^3+3\times6^2+3^3}{-13}=\frac{\left(2\times3\right)^3+3\times\left(3\times2\right)^2+3^3}{-13}=\frac{2^3\times3^3+3\times3^2\times2^2+3^3}{-13}=\frac{8\times3^3+3^3\times4+3^3}{-13}\)\(=\frac{3^3\times\left(8+4+1\right)}{-13}=\frac{27\times13}{-13}=-27\)
5 tháng 7 2016
a/ \(\frac{4^2.4^3}{2^{10}}=\frac{4^5}{2^{10}}=\frac{\left(2^5\right)^2}{2^{10}}=\frac{2^{10}}{2^{10}}=1\)
b/\(\frac{\left(0,6\right)^5}{\left(0,2\right)^6}=\frac{\left(0,6\right)^5}{\left(0,2\right)^5.\left(0,2\right)}=\left(\frac{0,6}{0,2}\right)^5.\frac{1}{\frac{1}{5}}=3^5.5=243.5=1215\)
c/ \(\frac{2^7.9^3}{6^5.8^2}=\frac{2^7.\left(3^2\right)^3}{\left(2.3\right)^5.\left(2^3\right)^2}=\frac{2^7.3^6}{2^5.3^5.2^6}=\frac{2^7.3.3^5}{2^7.2^4.3^5}=\frac{3}{16}\)
d/ \(\frac{6^3+3.6^2+3^3}{-13}=\frac{\left(2.3\right)^3+3.\left(2.3\right)^2+3^3}{-13}=\frac{2^3.3^3+3.2^2.3^2+3^3}{-13}=\frac{3^3.\left(2^3+2^2+1\right)}{-13}=\frac{27.13}{-13}=-27\)
PA
15 tháng 11 2016
II. Trắc Nghiệm
Câu 1: Cho x = | x| kết quả nào đúng sau đây
a. x = 0
b. x = 1
c. x > 0
d. x ≥ 0
Câu 2: Trong các phân số sau, phân số nào biểu diễn số hữu tỷ 2/-5?
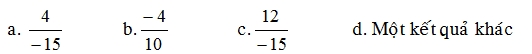
=> Chọn B
Câu 3: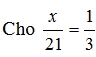 
giá trị của x bằng bao nhiêu?
a. 63
b. 1/7
c. 7
d. 0,7
Câu 4: 76 + 75 – 74 chia hết cho:
a. 5
b.7
c.11
d. Cả 3 số trên
Câu 5: Kết quả nào sau đây là đúng ?
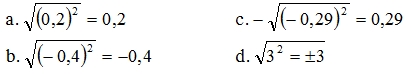
=> Chọn A
Câu 6: Câu nào trong các câu sau đây SAI
b. – 5 ∈ R
c. √4 ∈ I
d. N ⊂ R
15 tháng 11 2016
a) 4/3 x 2/5 - 3/4 x 2/5
= (4/3 - 3/4) x 2/5
= 7/12 x 2/5
= 7/30
b) 3 x ( -4/30)2 - 7/3
= 3 x 4/225 - 7/3
= 4/75 - 7/3
= -2,28
c) -0,8 x 1/9/25 - 4/5 x 64/25
= -4/5 x 1,36 - 4/5 x 2,56
= -4/5 x (1,36 - 2,56)
= -4/5 x (-1,2)
= 0,96
6 tháng 9 2017
a) \(\left(-\dfrac{2}{3}+\dfrac{3}{7}\right):\dfrac{4}{5}+\left(-\dfrac{1}{3}+\dfrac{4}{7}\right):\dfrac{4}{5}\)
= \(\left(-\dfrac{2}{3}+\dfrac{3}{7}-\dfrac{1}{3}+\dfrac{4}{7}\right):\dfrac{4}{5}\)
= \(0:\dfrac{4}{5}\)
= 0
b) \(\dfrac{5}{9}\left(\dfrac{1}{11}-\dfrac{5}{22}\right)+\dfrac{5}{9}\left(\dfrac{1}{15}-\dfrac{2}{3}\right)\)
= \(\dfrac{5}{9}:\left(\dfrac{1}{11}-\dfrac{5}{22}+\dfrac{1}{15}-\dfrac{2}{3}\right)\)
= \(\dfrac{5}{9}:-\dfrac{81}{110}\)
= \(-\dfrac{550}{729}\)
G
6 tháng 9 2017
Giải:
a) \(\left(\dfrac{-2}{3}+\dfrac{3}{7}\right):\dfrac{4}{5}+\left(\dfrac{-1}{3}+\dfrac{4}{7}\right):\dfrac{4}{5}\)
\(=\left[\left(\dfrac{-2}{3}+\dfrac{2}{7}\right)+\left(\dfrac{-1}{3}+\dfrac{4}{7}\right)\right]:\dfrac{4}{5}\)
\(=\left(\dfrac{-2}{3}+\dfrac{2}{7}-\dfrac{1}{3}+\dfrac{4}{7}\right):\dfrac{4}{5}\)
\(=\left(-1+1\right):\dfrac{4}{5}\)
\(=0:\dfrac{4}{5}\)
\(=0.\dfrac{4}{5}\)
\(=0\)
b) \(\dfrac{5}{9}:\left(\dfrac{1}{11}-\dfrac{5}{22}\right)+\dfrac{5}{9}:\left(\dfrac{1}{15}-\dfrac{2}{3}\right)\)
\(=\dfrac{5}{9}:\left(\dfrac{2}{22}-\dfrac{5}{22}\right)+\dfrac{5}{9}:\left(\dfrac{1}{15}-\dfrac{10}{15}\right)\)
\(=\dfrac{5}{9}:\dfrac{-3}{22}+\dfrac{5}{9}:\dfrac{-3}{5}\)
\(=\dfrac{5}{9}:\left(\dfrac{-3}{22}-\dfrac{3}{5}\right)\)
\(=\dfrac{5}{9}:\left(\dfrac{-3}{22}-\dfrac{3}{5}\right)\)
\(=\dfrac{5}{9}:\dfrac{-81}{110}\)
\(=-\dfrac{550}{729}\)
Chúc bạn học tốt!!!
TA
. tính 
0