Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Dễ thấy với a,b >0 thì (a+b)/2 ≥ √ab <=> 1/(a+b) ≤ 1/4 (1/a +1/b)
Áp dụng bất đẳng thức Cauchy ta được
1/(a+2b+3c)=1/[(a+c)+2(b+c)]≤ 1/4[1/(a+c)+1/2(b+c)] (lại áp dụng tiếp được)
≤ 1/16a+1/16c+1/32b+1/32c
=1/16a+1/32b+3/32c
Trường hợp này dấu "=" xảy ra <=> a+c=2(b+c);a=c;b=c <=> c= 0 mâu thuẩn giả thiết
Do đó dấu "=" không xảy ra
Thế thì 1/(a+2b+3c)<1/16a+1/32b+3/32c (1)
Tương tự 1/( b+2c+3a)<1/16b+1/32c+3/32a (2)
1/ ( c+2a+3b) < 1/16c+1/32a+3/32b (3)
Cộng (1)(2)(3) cho ta
1/( a+2b+3c) + 1/( b+2c+3a) + 1/ ( c+2a+3b) <(1/16+1/32+3/32)(1/a+1/b+1/c)
=3/16*(ab+bc+ca)abc= 3/16
tk nha mk trả lời đầu tiên đó!!!

1. \(a< b\Leftrightarrow2a< 2b\Leftrightarrow2a+1< 2b+1\)
\(a< b\Leftrightarrow-3a>-3b\Leftrightarrow-3a>-3b-1\)
2.\(a>b>0\Leftrightarrow a.\frac{1}{ab}>b.\frac{1}{ab}\Leftrightarrow\frac{1}{b}>\frac{1}{a}\Leftrightarrow\frac{1}{a}< \frac{1}{b}\)

1 ) Do \(3a-b=5\Rightarrow b=3a-5\)
Ta có : \(A=\frac{5a-b}{2a+5}-\frac{3b-3a}{2b-5}=\frac{5a-3a+5}{2a+5}-\frac{3\left(3a-5\right)-3a}{2\left(3a-5\right)-5}=\frac{2a+5}{2a+5}-\frac{6a-15}{6a-15}=1-1=0\)
Vậy \(A=0\)
2 ) \(P=x^4+x^2+1=\left(x^4+2x^2+1\right)-x^2=\left(x^2+1\right)^2-x^2=\left(x^2-x+1\right)\left(x^2+x+1\right)\)
Để P là số nguyên tố thì \(Ư\left(P\right)=\left\{1;P\right\}\)
Vì x dương \(\Rightarrow x^2+x+1>x^2-x+1\)
\(\Rightarrow x^2-x+1=1\)
\(\Rightarrow x\left(x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\left(L\right)\\x=1\end{matrix}\right.\)
Vậy x = 1 thì P là số nguyên tố

1 . a) Thực hiện so sánh 3a và 3b, 3a+1 và 3b+1 từ đó rút ra điêu cần chứng minh
b) Thực hiện so sánh -2a và -2b, -2a - 5 và -2b -5 từ đó rút ra điêu cần chứng minh
Cậu tự trình bày nhé ? Giảng sơ sơ thế là hiểu ấy

Dùng điểm rơi a=b=1
Gọi M là biểu thức đầu bài ta có
\(M=\frac{3}{2}\sqrt{\left(3a+1\right).4}+\sqrt{\left(3b+1\right).4}\le\frac{3}{4}\left(3a+5\right)+\frac{1}{2}\left(3b+5\right)\)
\(=\frac{9a+6b}{4}+\frac{25}{4}=\frac{15}{4}+\frac{25}{4}=10\)

a) Từ a + 5 < b + 5
=> a + 5 + (-5) < b + 5 + (-5) (cộng hai vế với -5)
=> a < b
a)từ a+5<b+5 ta cộng -5 vào 2 vế được a<b
b)từ -3a>-3b ta nhân 2 vế với -1/3 (tức là chia cả 2 vế cho -3) và -3a . -1/3< -3b . -1/3 sẽ được a<b
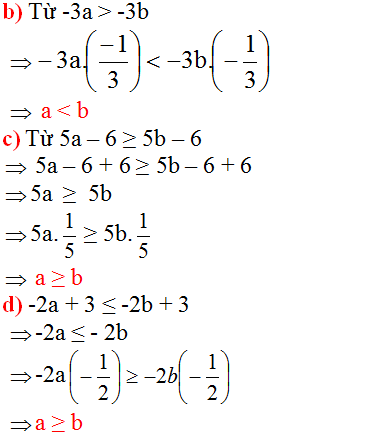
a) Ta có: 3a+1<3b+1
\(\Leftrightarrow3a< 3b\)
hay a<b
câu b nx bn ơi