Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Đồng vị X1 có tổng số hạt là 18 → 2Z1 + N1 = 18
Trong X1 có các loại hạt bằng nhau
→ Z1= N1 =
18
3
= 6 → A1 = Z1 + N1 = 12
Đồng vị X2 có tổng số hạt là 20
→ 2Z2 + N2 = 20
Luôn có Z2=Z1 ( cùng là đồng vị của nguyên tố X)
→ Z2 = 6 → N2 = 8 → A2 = 6 + 8 = 14
Nguyên tử khối trung bình của X là
M X = ( 50 . 12 + 20 . 14 ) / 100 = 13

Đáp án C
Các loại hạt trong X1 bằng nhau → pX1 = nX1 = 18 : 6
Vì X1 và X2 là đồng vị → pX1 =pX2 =6
Tổng số hạt trong X2 là 20 → 2pX2 + nX2 = 20 → nX2 = 8
Số khối của X1 là 12, số khối của X2 là 14
Nguyên tử khối trung bình của X là 50 . 12 + 50 . 14 100 . 100 = 13

Vì phần trăm các đồng vị bằng nhau nên mỗi đồng vị chiếm 50%.
Vì các loại hạt trong X1 bằng nhau và X1 có tổng số hạt (gồm p, n, e) là 18
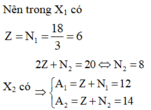
Vậy nguyên tử khối trung bình của X là:
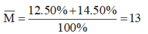
Đáp án D

Đáp án D
Vì phần trăm các đồng vị bằng nhau nên mỗi đồng vị chiếm 50%.
Vì các loại hạt trong X1 bằng nhau và X1 có tổng số hạt (gồm p, n, e) là 18
Nên trong X1 có Z = N 1 = 18 3 = 6
X2 có 2 Z + N 2 = 20 ⇔ N 2 = 8 ⇒ A 1 = Z + N 1 = 12 A 2 = Z + N 2 = 14
Vậy nguyên tử khối trung bình của X là:
M
¯
=
12
.
50
%
+
14
.
50
%
100
%
=
13

Đáp án D.
X1 có tổng các loại hạt bằng = 18 và các hạt trong X1 bằng nhau
Ta có p + e + n = 18 mặt khác p = e =n
=> p = e = n =6
X2 có số hạt proton bằng số hạt proton trong X1 do cùng là đồng vị:
2p + n =20 => n = 8
Ta có số khối của X1 = 12, X2 = 14 và %X1 = %X2 = 50%.
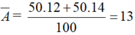

Đồng vị X1 có tổng số hạt là 18 → 2Z1 + N1 = 18
Trong X1 có các loại hạt bằng nhau
→ Z1= N1 = 18 3 = 6 → A1 = Z1 + N1 = 12
Đồng vị X2 có tổng số hạt là 20
→ 2Z2 + N2 = 20
Luôn có Z2=Z1 ( cùng là đồng vị của nguyên tố X)
→ Z2 = 6 → N2 = 8 → A2 = 6 + 8 = 14
Nguyên tử khối trung bình của X là
M X = ( 50 . 12 + 20 . 14 ) / 100 = 13

Đáp án D
Gọi p là số proton của X.
n1 và n2 lần lượt là số nơtron của X1 và X2
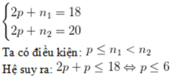
![]()
![]()
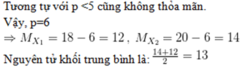

Có
+) 2pY + nY = 43
+) \(2p_Y=\dfrac{28}{15}n_Y\)
=> \(\left\{{}\begin{matrix}p_Y=14\\n_Y=15\end{matrix}\right.\) => AY = 14 + 15 = 29 => AX = 28
=> \(\overline{M}=\dfrac{28.90+29\left(100-90\right)}{100}=28,1\)