Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài giải:
a) Gọi đường chéo của hình vuông có độ dài là a.
Ta có: a2 = 32 + 32 = 18
Suy ra a = √18
Vậy đường chéo của hình vuông đó bằng 3√2.
b) Gọi cạnh của hình vuông là a.
Ta có a2 + a2 + 22 =>2 a2 = 4 => a2 = 2 => a = √2
Vậy cạnh của hình vuông đó bằng √2
Ta có: a2 = 32 + 32 = 18
Suy ra a = √1818
Vậy đường chéo của hình vuông đó bằng 3√22.
b) Gọi cạnh của hình vuông là a.
Ta có a2 + a2 + 22 =>2 a2 = 4 => a2 = 2 => a = √22
Vậy cạnh của hình vuông đó bằng √22.

a)
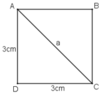
Gọi đường chéo của hình vuông có độ dài là a.
Áp dụng định lí Pi-ta-go ta có:
a2 = 32 + 32 = 18 suy ra a = √18 = 3√2
Vậy đường chéo của hình vuông đó bằng 3√2 (cm)
b)
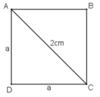
Gọi cạnh của hình vuông là a.
Áp dụng định lí Pi-ta-go ta có:
a2 + a2 = 22 ⇒ 2a2 = 4
⇒ a2 = 2 ⇒ a = √2
Vậy cạnh của hình vuông đó bằng √2 (dm).


A B C D a
Gọi đường chéo của hình vuông có độ dài là a.
Áp dụng định lí Pi-ta-go ta có:
a2 = 32 + 32 = 18 suy ra a = √18
Vậy đáp án là √18 cm
Gọi 4 đỉnh của hình vuông là A,B,C,D.
Xét tam giác ABC có \(\widehat{B}\)=90o(ABCD là hình vuông)=> tam giác ABC vuông tại B
Theo định lí Pytago, ta có:
AC2=BD2=32+32=18
=>AC=BD=\(\sqrt{18}\)(cm)
=>đpcm
Hok tốt#

Độ dài đường chéo là ( áp dụng định lý Pitago cho tam giác vuông ADC ):
AC2 = 2CD2 (vì AD = CD)
=> AC2 = \(\left(3\sqrt{2}\right)^2\) = 18
=> AC = \(\sqrt{18}\)

Tia AB cắt DC tại E.
=> AC là tia phân giác của \(\widehat{DAE}\left(gt\right)\)
\(\Rightarrow AC\perp DE\left(gt\right)\)
=> Tam giác ADE cân.
Lại có: \(\widehat{D}=60^o\Rightarrow\Delta ADE\) là tam giác đều.
=> C là trung điểm DE (AC đồng thời la trung tuyến)
Mà: BC//AD => BC là đường trung bình của \(\Delta ADE\)
Ta có: \(AB=DC=\frac{AD}{2},BC=\frac{AD}{2}\)
Giả thiết: \(AB+BC+CD+AD=20\)
\(\Rightarrow\frac{AD}{2}+\frac{AD}{2}+\frac{AD}{2}+AD=20\)
\(\Rightarrow\frac{5}{2}AD=20\Rightarrow AD=8\left(cm\right)\)
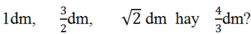
a, \(\sqrt{18}\)cm
b, \(\sqrt{2}\)dm