Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét phương trình tiếp tuyến tổng quát có dạng:
\(y=\left(6x_0+3x_0^2\right)\left(x-x_0\right)+3x_0^2+x_0^3\)
có 3 tiếp tuyến đi qua A(a,0) nên phương trình \(\left(6x_0+3x_0^2\right)\left(a-x_0\right)+3x_0^2+x_0^3=0\) có 3 nghiệm
\(PT\Leftrightarrow\orbr{\begin{cases}x_0=0\\2x_0^2+3\left(1-a\right)x_0+6a=0\end{cases}}\)
Vậy có 1 pttt là y=0
do đó để có hai tiếp tuyến vuông góc thì \(2x_0^2+3\left(1-a\right)x_0+6a=0\) có hia nghiệm \(x_1,x_2\text{ thỏa mãn}\)
\(\left(6x_1+3x_1^2\right)\left(6x_2+3x_2^2\right)=-1\)mà áp dung Viet ta có \(\hept{\begin{cases}x_1+x_2=\frac{3a-3}{2}\\x_1x_2=3a\end{cases}}\)
Nên \(36x_1x_2+18x_1x_2\left(x_1+x_2\right)+9x_1^2x_2^2=-1\Leftrightarrow126a+81a\left(a-1\right)+81a^2=-1\)
từ đây mình giải được a nhé
Xét phương trình tiếp tuyến tổng quát có dạng:
y=(6x0+3x02)(x−x0)+3x02+x03
có 3 tiếp tuyến đi qua A(a,0) nên phương trình (6x0+3x02)(a−x0)+3x02+x03=0 có 3 nghiệm
PT⇔[
| x0=0 |
| 2x02+3(1−a)x0+6a=0 |
Vậy có 1 pttt là y=0
do đó để có hai tiếp tuyến vuông góc thì 2x02+3(1−a)x0+6a=0 có hia nghiệm x1,x2 thỏa mãn
(6x1+3x12)(6x2+3x22)=−1mà áp dung Viet ta có {
| x1+x2=3a−32 |
| x1x2=3a |
Nên 36x1x2+18x1x2(x1+x2)+9x12x22=−1⇔126a+81a(a−1)+81a2=−1

a)  (x4 – x2 + x - 1) =
(x4 – x2 + x - 1) =  x4(1 -
x4(1 - 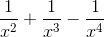 ) = +∞.
) = +∞.
b)  (-2x3 + 3x2 -5 ) =
(-2x3 + 3x2 -5 ) =  x3(-2 +
x3(-2 + 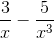 ) = +∞.
) = +∞.
c) 
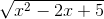 =
= 
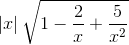 = +∞.
= +∞.
d) 
 =
= 

= 
 =
= 
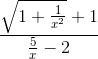 = -1.
= -1.

xAB + ABE
= 400 + 1400
= 1800
=> xAB và ABE là 2 góc bù nhau
mà 2 góc này ở vị trí trong cùng phía
=> Ax // DE
=> xAB = DBA
mà xAB = 400 (gt)
=> DBA = 400
BCy + CBD = 1800 (2 góc trong cùng phía, DE // Cy)
1300 + CBD = 1800
CBD = 1800 - 1300
CBD = 500
mà DBA = 400 (chứng minh trên)
=> CBD + DBA = 500 + 400 = 900
=> ABC = 900
=> AB _I_ BC
xAB + ABE
= 400 + 1400
= 1800
=> xAB và ABE là 2 góc bù nhau
mà 2 góc này ở vị trí trong cùng phía
=> Ax // DE
=> xAB = DBA
mà xAB = 400 (gt)
=> DBA = 400
BCy + CBD = 1800 (2 góc trong cùng phía, DE // Cy)
1300 + CBD = 1800
CBD = 1800 - 1300
CBD = 500
mà DBA = 400 (chứng minh trên)
=> CBD + DBA = 500 + 400 = 900
=> ABC = 900
=> AB _I_ BC

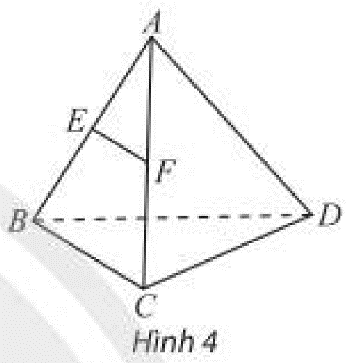






 . Tính
. Tính 

 .
. . Tính
. Tính  bằng:
bằng:
 bằng:
bằng:

 .
.


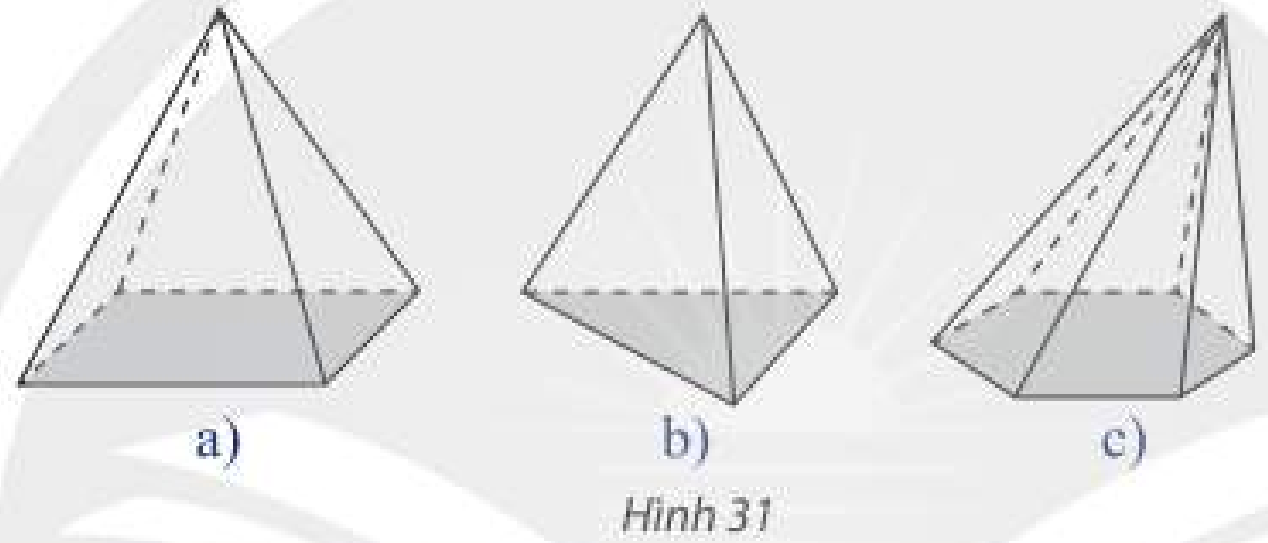
Các công trình kiến trúc, đồ vật có trong hình 30 có mặt bên là hình tam giác.