Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

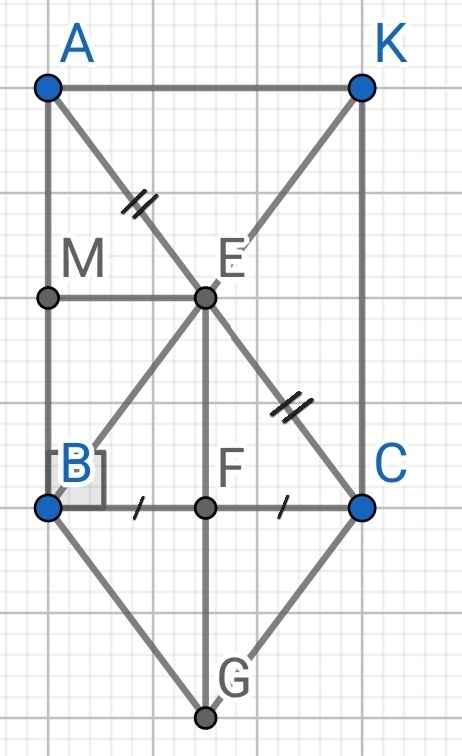
a) ∆ABC vuông tại B (gt)
⇒ AB ⊥ BC
⇒ BM ⊥ BF
⇒ ∠MBF = 90⁰
Do EM // BC (gt)
⇒ EM // BF
EM // BC (gt)
E là trung điểm của AC (gt)
⇒ M là trung điểm của AB
⇒ EM là đường trung bình của ∆ABC
⇒ EM = BC : 2
F là trung điểm của BC (gt)
⇒ BF = CF = BC : 2
⇒ EM = BF = BC : 2
Tứ giác BMEF có:
EM // BF (cmt)
EM = BF = BC : 2 (cmt)
⇒ BMEF là hình bình hành
Mà ∠MBF = 90⁰ (cmt)
⇒ BMEF là hình chữ nhật
b) Do K đối xứng với B qua E (gt)
⇒ E là trung điểm của BK
Tứ giác BAKC có:
E là trung điểm của BK (cmt)
E là trung điểm của AC (gt)
⇒ BAKC là hình bình hành
Mà ∠ABC = 90⁰ (gt)
⇒ BAKC là hình chữ nhật
c) Do G đối xứng với E qua F (gt)
⇒ F là trung điểm của EG
∆ABC vuông tại B (gt)
E là trung điểm của AC (gt)
⇒ BE là đường trung tuyến ứng với cạnh huyền AC
⇒ BE = CE = AC : 2
Tứ giác BGCE có:
F là trung điểm của BC (gt)
F là trung điểm của EG (cmt)
⇒ BGCE là hình bình hành
Mà BE = CE (cmt)
⇒ BGCE là hình thoi
d) Để BGCE là hình vuông thì BE ⊥ CE
⇒ BE là đường cao của ∆ABC
Mà BE là đường trung tuyến của ∆ABC (cmt)
⇒ ∆ABC cân tại B
Lại có ∆ABC vuông tại B (gt)
⇒ ∆ABC vuông cân tại B
\(a,\left\{{}\begin{matrix}BF=CF\\CE=EA\end{matrix}\right.\Rightarrow EF\) là đtb tam giác ABC
\(\Rightarrow EF=\dfrac{1}{2}AB;EF//AB\Rightarrow EF//BM\)
Mà \(ME//BF\) nên BMEF là hbh
Mà \(\widehat{ABC}=90^0\) nên BMEF là hcn
\(b,\left\{{}\begin{matrix}BE=EK\\AE=EC\\\widehat{ABC}=90^0\end{matrix}\right.\Rightarrow BAKC\) là hcn
\(c,\left\{{}\begin{matrix}EF=FG\\CF=BF\end{matrix}\right.\Rightarrow BGCE\) là hbh
Mà \(CE=BE\left(t/c.hình.chữ.nhật.BAKC\right)\)
Vậy BGCE là hình thoi
\(d,BGCE\) là hình vuông \(\Leftrightarrow\widehat{CEB}=90^0\Leftrightarrow CE\perp BE\)
\(\Leftrightarrow BE\) là đường cao tam giác ABC
Mà BE là trung tuyến tam giác ABC
Do đó tam giác ABC phải vuông cân
Vậy BGCE là hình vuông \(\Leftrightarrow\) tam giác ABC vuông cân

a: Sửa đề: Ex//BC, Ex cắt AC tại M
a: Xét ΔABC có
E là trung điểm của BA
EM//BC
=>M là trung điểm của AC
Xét ΔCAB có
E,M lần lượt là trung điểm của AB,AC
=>EM là đường trung bình
=>EM=1/2BC
=>EM=BF
Xét tứ giác EMFB có
EM//FB
EM=FB
góc FBE=90 độ
Do đó: EMFB là hình chữ nhật
b: Sửa đề: K đối xứng B qua M
Xét tứ giác BAKC có
M là trung điểm chung của BK và AC
góc ABC=90 độ
=>BAKC là hình chữ nhật
c: Xét tứ giác BGCE có
F là trung điểm chung của BC và GE
=>BGCE là hình bình hành

a: Xét ΔABC có
D là trung điểm của BC
E là trung điểm của AB
Do đó: DE là đường trung bình
=>DE//FA và DE=FA
hay AEDF là hình bình hành

Bạn tự vẽ hình nha
Do He vuông góc AC -> góc HEA=góc HEC
HD vuông AB -> góc HDB=góc HDA
Xét tứ giác AEHD có
góc HEA = 90 độ( cmt)
góc HDA= 90 độ(cmt)
góc DAE= 90 độ( tam giác ABC vuông tại A)
-> tứ giác AEHD là hình chữ nhật( dấu hiệu tứ giác có 3 góc vuông)

A F E D B C M
Mình vẽ hình hơi xâu, bạn thông cảm nhé!
a) Xét từ giác ABMC có: + AM cắt BC tại D (bạn dùng ký hiệu giao nhé)
+ DA = DM (gt)
+ DB = DM(gt)
suy ra, tứ giác AMCM là hình bình hành mà ta có góc CAB là góc vuông suy ra tứ giác ABMC là hình chữ nhật
Các câu còn lại bạn đầu có thể giải theo cách trên nhé!
( e mk chưa làm đc, mk mới đc học đến bào hình chữ nhật thôi, sory)

Hình tự vẽ dc ko ạ =(((( mik vẽ r nhưng lại bị out ra =.= lười lắm ạ
A/ xét tg AEHF ta có : HE vuông góc AB, FA vuông góc AB, HE//AC (gt)
=> góc AEH = góc EAF = góc AFH = 90 độ
=> Tứ giác AEHF là HCN
=>AH=EF
B/ Ta có H đối xứng M qua E => ME=EH
mak EH= AF (hcn) => ME=À
Ta có H đối xứng vs N qua F => FH=FN
mak FH =EA (hcn) => FN=EA
Xét tứ giác MEFA có :
+ ME=AF
+ ME//AF( slt)
=>Tứ giác MEFA là hình bình hành
=>EF=MA,EF//MA (1)
Xét tứ giác EFAN có :
+ FN = EA
+ AE//FN (slt)
=>Tứ giác EFAN là hình bình hành
=>EF=AN.EF//AN(2)
Từ (1) và (2) => MA=AN ; A,M,N thẳng hàng
=> M đối xứng N qua A
Ak quên câu C =.= ko thấy .V
C/Ta có M đối xứng H qua AB
=> AB là đg trung trực
=>MB=HB;MA=HA
Xét tam giác ABM và tam giác HAB có
BM=BH
MA=MH
AB chung
=>tam giác ABM = tam giác HAB (c-c-c)
=) góc M = góc H =90độ
Ta có H đối xứng N qua AC
=> AC là đg trung trực
=>HC=CN;HA=AN
Xét tam giác HCA và Tam giác ACN
HC=CN
HA=AN
AC chung
=>tam giác HCA = Tam giác ACN (c-c-c)
=) góc H= góc N =90 độ
Có CN vuông góc HA vuông góc BM
=> BM//CN
=> MBCN là hình thang mak góc BMN =90 đố => MBCN là hình thang vuông (dpcm)