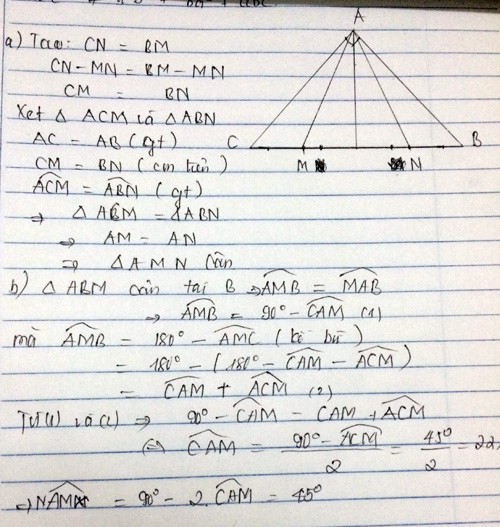
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A C B D E O N M
a) Ta có \(\widehat{B}+\widehat{C}=90^o\) mà \(\widehat{B_1}=\widehat{B_2}=\frac{\widehat{B}}{2};\widehat{C_1}=\widehat{C_2}=\frac{\widehat{C}}{2}\) nên \(\widehat{B_2}+\widehat{C_2}=\frac{\widehat{B}+\widehat{C}}{2}=\frac{90^o}{2}=45^o\)
Xét tam giác BOC, có \(\widehat{BOC}+\widehat{B_2}+\widehat{C_2}=180^o\Rightarrow\widehat{BOC}=180^o-45^o=135^o\)
b) Xét tam giác BAD và BMD có:
Cạnh BD chung
\(\widehat{B_1}=\widehat{B_2}\)
AB = MB (gt)
\(\Rightarrow\Delta BAD=\Delta BMD\left(c-g-c\right)\)
\(\Rightarrow\widehat{BMD}=\widehat{BAD}=90^o\)
Hoàn toàn tương tự \(\Delta EAC=\Delta ENC\left(c-g-c\right)\Rightarrow\widehat{ENC}=\widehat{EAC}=90^o\)
Ta có EN và DM cùng vuông góc với BC nên EN // DM
c) Theo câu b, \(\Delta BAD=\Delta BMD\Rightarrow AD=MD;\widehat{BDA}=\widehat{BDM}\)
Từ đó ta có \(\Delta OAD=\Delta OMD\left(c-g-c\right)\Rightarrow OA=OM.\)
Tương tự : \(\Delta OAE=\Delta ONE\left(c-g-c\right)\Rightarrow OA=ON.\)
Vậy nên OA = OM = ON
d) Ta có \(\Delta OAD=\Delta OMD\left(c-g-c\right)\Rightarrow\widehat{OAD}=\widehat{OMD}\)
\(\Delta OAE=\Delta ONE\left(c-g-c\right)\Rightarrow\widehat{OAE}=\widehat{ONE}\)
\(\Rightarrow\widehat{ONE}+\widehat{OMD}=\widehat{OAE}+\widehat{OAD}=\widehat{EAD}=90^o\)
\(\Rightarrow\widehat{NOM}=90^o\) (Dạng bài qua O kẻ đường thẳng song song với EN và DM)
Vậy tam giác OMN vuông cân hay \(\widehat{ONM}+\widehat{OMN}=90^o\)
Xét tam giác AMN có \(\widehat{MAN}+\widehat{ANM}+\widehat{AMN}=180^o\)
\(\Leftrightarrow\widehat{MAN}+\widehat{ANO}+\widehat{ONM}+\widehat{AMO}+\widehat{OMN}=180^o\)
\(\Leftrightarrow\widehat{MAN}+\widehat{NAO}+\widehat{MAO}=180^o-90^o=90^o\)
\(\Leftrightarrow\widehat{2MAN}=90^o\)
\(\Leftrightarrow\widehat{MAN}=45^o\)

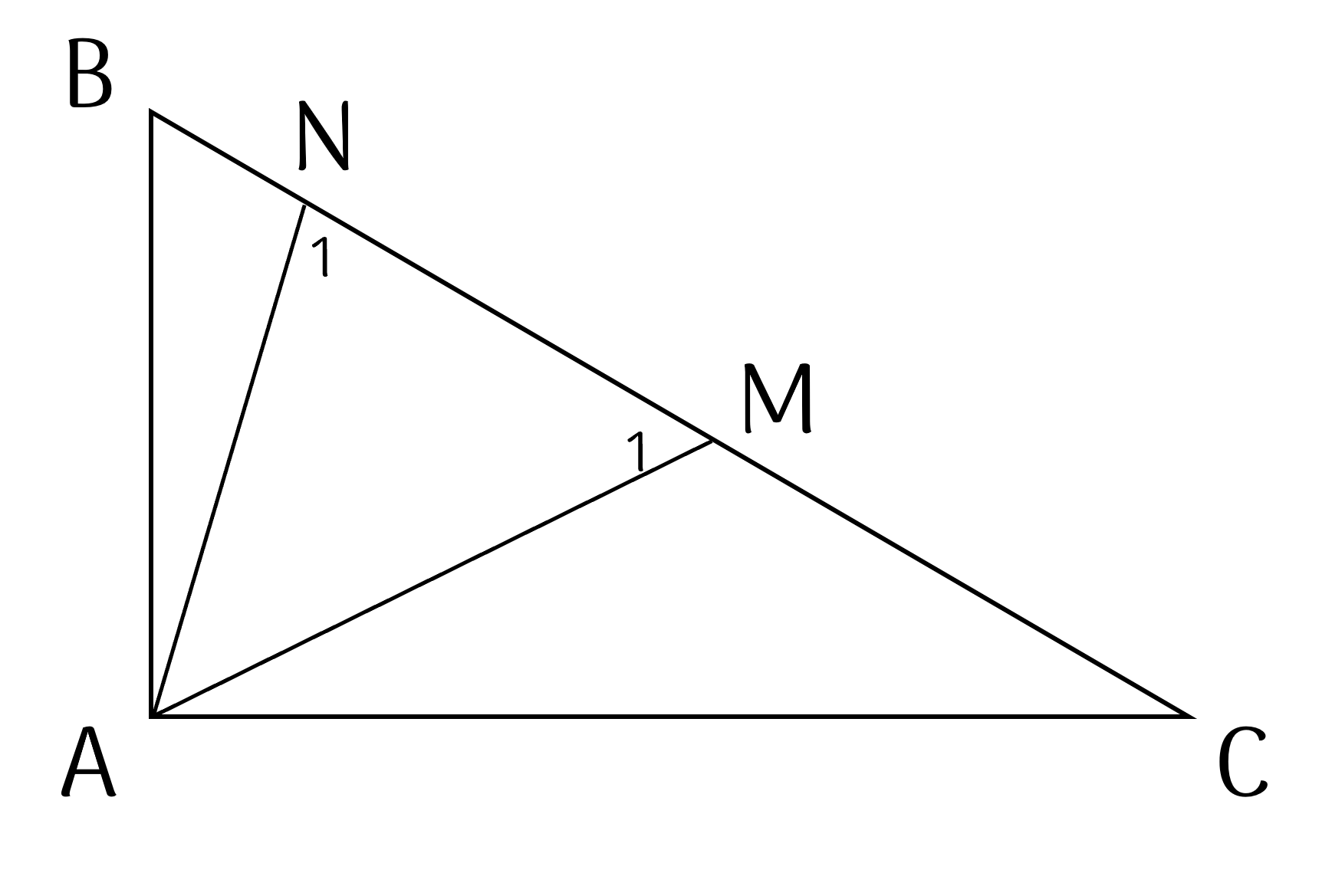
$BM = BA$ nên $\Delta BAM$ cân tại $B$.
Suy ra $\widehat{M_1} = \dfrac{180^{\circ} - \widehat{B}}2$.
$CN = CA$ nên $\Delta CAN$ cân tại $C$.
Suy ra $\widehat{N_1} = \dfrac{180^{\circ} - \widehat{C}}2$.
Suy ra $\widehat{N_1} + \widehat{M_1} = 180^{\circ} - \dfrac12(\widehat{B} + \widehat{C})$
nên $180^{\circ} - \widehat{N_1} - \widehat{M_1} = \dfrac12(\widehat{B} + \widehat{C})$
Trong $\Delta MAN$ có $\widehat{MAN} = 180^{\circ} - \widehat{N_1} - \widehat{M_1}$
nên $\widehat{MAN} = \dfrac12(\widehat{B} + \widehat{C}) = \dfrac12.90^{\circ} = 45^{\circ}$.

A B C M N
Ta có
BM=AB suy ra tam giác BAM cân tại B suy ra \(\widehat{BAM}=\frac{180^o-\widehat{B}}{2}\)
CN=AC suy ra tam giác NAC cân tại C suy ra \(\widehat{NAC}=\frac{180^o-\widehat{C}}{2}\)
(nếu cần thì bạn phải cm thêm cả N nằm giữa B và M nhé!)
MÀ ta thấy \(\widehat{BAM}+\widehat{ACN}=\widehat{BAC}+\widehat{NAM}\)
\(\Rightarrow\frac{180^o-\widehat{B}}{2}+\frac{180^o-\widehat{C}}{2}=90^o+\widehat{NAM}\)
\(\Rightarrow\frac{360^o-\left(\widehat{B}+\widehat{C}\right)}{2}=90^o+\widehat{NAM}\)
\(\Rightarrow\frac{360^o-90^o}{2}=90^o+\widehat{NAM}\)
\(\Rightarrow\widehat{NAM}=45^o\)

~ Tự vẽ hình nha ~
Chứng minh :
a) BD là phân giác của \(\widehat{ABC}\) ⇒ \(\widehat{ABD}=\widehat{CBD}=\dfrac{\widehat{ABC}}{2}\)
CE là phân giác của \(\widehat{BCA}\) ⇒ \(\widehat{ACE}=\widehat{BCE}=\dfrac{\widehat{ACB}}{2}\)
\(\Rightarrow\widehat{CBD}+\widehat{BCE}=\dfrac{\widehat{ABC}}{2}+\dfrac{\widehat{BCA}}{2}=\dfrac{\widehat{ABC}+\widehat{BCA}}{2}=\dfrac{90^o}{2}=45^o\)
Có \(\widehat{BOC}+\widehat{OBC}+\widehat{BCO}=180^o\text{ ( đ/l tổng 3 góc của 1 tam giác )}\)⇒ \(\widehat{BOC}+45^o=180^o\)
⇒ \(\widehat{BOC}=180^o-45^o\)
⇒ \(\widehat{BOC}=135^o\)
b) Xét △BDA và △BDM có :
BA = BM ( gt )
\(\widehat{ABD}=\widehat{MBD}\text{ ( gt )}\)
BD - cạnh chung
⇒ △BDA = △BDM ( c.g.c )
⇒ \(\widehat{BAD}=\widehat{BMD}\text{ ( tương ứng )}\)
⇒ \(\widehat{BMD}\text{ }=90^o\)
Tương tự :
△EAC=△ENC ( c.g.c)
⇒ \(\widehat{EAC}=\widehat{ENC}\text{ ( tương ứng )}\)
Có \(\widehat{DMN}+\widehat{ENM}=90^o+90^o=180^o\)
Mà \(\widehat{DMN}\text{ và }\widehat{ENM}\text{ là 2 góc trong cùng phía }\)
⇒ EN // DM