
| xy | \(6x^2y\) | \(5x^2y\) |
| xy | \(12x^3y^2\) | \(15x^3y^2\) |
| xy | \(2x^2y\) | \(-x^2y\) |
| xy | \(xy^3\) | \(\dfrac{-1}{2}xy^3\) |
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

| xy | \(6x^2y\) | \(5x^2y\) |
| xy | \(12x^3y^2\) | \(15x^3y^2\) |
| xy | \(2x^2y\) | \(-x^2y\) |
| xy | \(xy^3\) | \(\dfrac{-1}{2}xy^3\) |

|
Đơn thức |
Đơn thức thu gọn |
Bậc của biến x | Bậc của đơn thức | hệ số |
| 23zxy(3xy) | 24zx2y2 | 2 | 5 |
24 |
| 4y2x2(-1/2xy2z)2 | -x4y6z2 | 4 | 12 | -1 |
| 3(2y)(3y2)(xy)(x2y2) | 18y6x3 | 3 | 9 | 18 |

Từ hàm số đã cho, lần lượt thay các giá trị x, y đã cho trong bảng vào hàm sôs trên để tìm các giá trị còn lại. Ta được bảng sau:
|
x |
-0,5 |
-3 |
0 |
4,5 |
9 |
|
y |
−13−13 |
-2 |
0 |
3 |
6 |

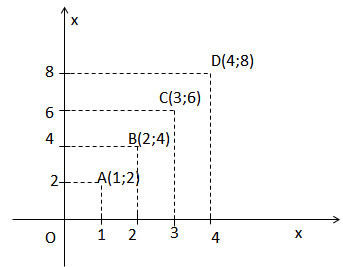
a) Tất cả các cặp giá trị tương ứng (x;y) là: (0;0), (1;2); (2; 4); (3; 6); (4; 8).
b) Trên hình vẽ 0, A, B, C, D là vị trí của các điểm biểu diễn các cặp giá trị tương ứng của x và y trong câu a.
a) Tất cả các cặp giá trị tương ứng (x;y) là: (0;0), (1;2); (2; 4); (3; 6); (4; 8).
b) Trên hình vẽ 0, A, B, C, D là vị trí của các điểm biểu diễn các cặp giá trị tương ứng của x và y trong câu a.


| Đơn thức | Đơn thức thu gọn | Bậc của biến x | Bậc của đơn thức | Hệ số của đơn thức |
| \(2^3zxy\left(3xy\right)\) | 24x2y2z | 2 | 5 | 24 |
| \(4y^2x^2\left(-\dfrac{1}{2}xy^2z\right)^2\) |
x4y6z2 |
4 | 12 | 1 |
| \(3\left(2y\right)\left(3y^2\right)\left(xy\right)\left(x^2y^2\right)\) | 18x3y6 | 3 | 9 | 18 |

Vì x và y là hai đại lượng tỉ lệ nghịch nên xy = a
Khi \(x=2,5\) thì \(y=-4\Rightarrow a=2,5.\left(-4\right)=-10\Rightarrow y=\dfrac{-10}{x}\)
Vậy \(x=\dfrac{-10}{y}\)
Kết quả như sau:
|
x |
1 |
2,5 |
4 |
5 |
8 |
10 |
|
y |
-10 |
-4 |
-2,5 |
-2 |
-1,25 |
-1 |

Theo đề bài, x và y là hai đại lượng tỉ lệ thuận nên y = kx
Mà khi x =-1 thì y = 2 nên 2 = k.(-1) ⇒⇒ k = -2
Ta điền vào bảng sau:
|
x |
-2 |
-1 |
1 |
3 |
4 |
|
y |
4 |
2 |
-2 |
-6 |
-8 |
x và y tỉ lệ thuận nên y = k.x
Từ đó ta tìm được y lần lượt là:
(-2).(-3) = 6 ; (-2) (-1) = 2;
(-2).1 = (-2) ; (-2).5 = -10
Ta được bảng sau
| x | -3 | -1 | 1 | 2 | 5 |
| y | 6 | 2 | -2 | -4 | -10 |

| Đơn thức | Đa thức | Phân thức |
| \(xy^2;0;5x^2y;0,5xy^2;3;15\) | \(xy^2;\left(p-q\right)+3;0;5x^2y;3+2;0,5xy^2;3;15\) | \(xy^2;\left(p-q\right)+3;0;5x^2y;3+2;0,5xy^2;\frac{1}{2};\frac{\left(3x-5y\right)\cdot2}{3xy-z^2+1};15;\frac{5a-2b}{3k\cdot7k+5}\) |
Chú ý :
Mỗi đơn, đa thức cúng được coi như một phân thức với mẫu thức bằng 1.
VD : \(xy=\frac{xy}{1};2(5a-b)=\frac{2\left(5a-b\right)}{1};2x^3y^2z^4+1=\frac{2x^3y^2z^4+1}{1}.\)