
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có:
\(115\%x+110\%\left(900-x\right)=1010\)
\(\Leftrightarrow\dfrac{115}{100}x+\dfrac{110}{100}.\left(900-x\right)=1010\)
\(\Leftrightarrow\dfrac{115}{100}x+990-\dfrac{110}{100}x=1010\)
\(\Leftrightarrow\dfrac{5}{100}x=20\)
\(\Rightarrow x=400\)
Vậy phương trình có nghiệm duy nhất là x=400

\(\hept{\begin{cases}39x+2y=400\\x+y+x^2=115\end{cases}}\)
\(\hept{\begin{cases}39x=400-2y\\x+y+x^2=115\end{cases}}\)
\(\hept{\begin{cases}x=400-\frac{2y}{39}\\x+y+x^2=115\end{cases}}\)
Ta thay 400 - 2y/39 vào biểu thức x + y + x^2 ta đc
\(400-\frac{2y}{39}+y+\left(400-\frac{2y}{39}\right)^2=115\)
\(400-\frac{41y}{39}+4\left(200-\frac{y}{39}\right)^2=115\)
\(400-4y+4\left(4000-\frac{400y}{39}+\frac{y^2}{1521}\right)=115\)
\(400-4y+16000-\frac{1600y}{39}+\frac{4y^2}{1521}=115\)
\(16400-4y-\frac{1600y}{39}+\frac{4y^2}{1521}=115\)
\(4y-\frac{1600y}{39}+\frac{4y^2}{1521}=16285\)
\(4y-\frac{1600y}{39}+\frac{4y^2}{1521}-16285=0\)
\(56316y-4y^2+24769485=0\)
Vậy hpt vô nghiệm :)
\(\hept{\begin{cases}39x+2y=40\\x+y+x^2=115\end{cases}}\)
\(< =>\hept{\begin{cases}400-2y=39x\\x+y+x^2=115\end{cases}}< =>\hept{\begin{cases}x=\frac{400-2y}{39}\\\frac{400-2y}{39}+y+\left(\frac{400-2y}{39}\right)^2=115\end{cases}}\)
\(< =>\frac{400-2y}{39}+\frac{39y}{39}+\frac{400^2-2.400.2y+4y^2}{39^2}=\frac{4485}{39}\)
\(< =>400-2y+39y+\frac{160000-1600y+4y^2}{39}=4485\)
\(< =>37y+\frac{4\left(40000-400y+y^2\right)}{39}=4085\)
\(< =>\frac{1443y+4\left[40000-y\left(400-y\right)\right]}{39}=\frac{159315}{39}\)
\(< =>1443y+160000+1600y+4y^2=159315\)
\(< =>3043y+4y^2=-685\)\(< =>4y^2+3043y-685=0\)
Ta có : \(\Delta=3043^2-4.4.\left(-685\right)=9259849+10960=9270809\)
Do delta > 0 nên pt có 2 nghiệm phân biệt !
\(y_1=\frac{-3043+\sqrt{9270809}}{8}=0,2250402=0,225\)
\(y_2=\frac{-3043-\sqrt{9270809}}{8}=-760,9750402=-760,975\)
Vậy ...
Bạn viruss corona phân tích sai thì có xD
Toàn lấy từ trên trời xuống cái j ko đâu hết !

\(110\%x+115\%y=400\\ \Rightarrow1.1x+1.15y=400\\ x+y=360\\ \Leftrightarrow1.1\left(x+y\right)=360\cdot1.1=396\\ \Rightarrow\left(1.1x+1.15y\right)-1.1\left(x+y\right)=1.1x+1.15y-1.1x-1.1y=0.05y=4\\ \Leftrightarrow y=\dfrac{4}{0.05}=80\\ \Rightarrow x=360-80=280.\)

Để pt có 2 nghiệm x1,x2 thì \(\Delta'=\left(m-1\right)^2-\left(m^2+m+4\right)=-3m-3\ge0\)
<=>\(m\le-1\)
Khi đó, theo hệ thức Vi-et thì: \(\hept{\begin{cases}x_1+x_2=2\left(m-1\right)\\x_1x_2=m^2+m+4\end{cases}}\)
\(x_1^2+x_2^2=\left(x_1+x_2\right)^2-2x_1x_2=\left(2m-2\right)^2-2\left(m^2+m+4\right)\)
\(=2m^2-10m-4=2\left(m-\frac{5}{2}\right)^2-\frac{33}{2}\ge\frac{-33}{2}\)
Dấu "=" xảy ra khi \(\left(m-\frac{5}{2}\right)^2=0\Leftrightarrow m-\frac{5}{2}=0\Leftrightarrow m=\frac{5}{2}\)(ko thoả mãn \(m\le-1\))
Vậy ko tìm đc m thỏa mãn
Để pt có 2 nghiệm khi \(\Delta\ge0\)
\(\Delta=\left(2m-2\right)^2-4\left(m^2+m+4\right)=4m^2-8m+4-4m^2-4m-16\)
\(=-12m-12\ge0\Leftrightarrow m\le1\)
Theo Vi et ta có : \(\hept{\begin{cases}x_1+x_2=-\frac{b}{a}=2m-2\\x_1x_2=\frac{c}{a}=m^2+m+4\end{cases}}\)
mà \(\left(x_1+x_2\right)^2=4m^2-8m+4\Rightarrow x_1^2+x_2^2=4m^2-8m+4-2m^2-2m-8\)
\(x_1^2+x_2^2=2m^2-10m-4=2\left(m^2-5m-2\right)=2\left(m^2-5.\frac{2}{5}m+\frac{4}{25}-\frac{54}{25}\right)\)
\(=2\left(m-\frac{2}{5}\right)^2-\frac{108}{25}\ge-\frac{108}{25}\)
Dấu ''='' xảy ra khi \(m=\frac{2}{5}\)( tmđk )
Vậy GTNN biểu thức trên là \(-\frac{108}{25}\)khi m =2/5

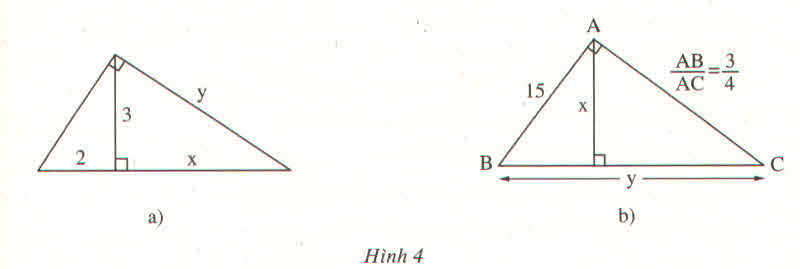
a) Áp dụng hệ thức lượng trong tam giác vuông⇒32=2x⇒x=\(\dfrac{9}{2}=4,5\)
Áp dụng định lý Pi-ta-go⇒y2=32+x2=9+20,25=29,25⇒\(y=\dfrac{3\sqrt{13}}{2}\)
b) Ta có \(\dfrac{AB}{AC}=\dfrac{3}{4}\Rightarrow AC=\dfrac{4}{3}.AB=\dfrac{4}{3}.15=20\)
Áp dụng hệ thức lượng trong tam giác vuông ⇒\(\dfrac{1}{x^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}=\dfrac{1}{225}+\dfrac{1}{400}=\dfrac{1}{144}\Rightarrow x^2=144\Rightarrow x=12\)Áp dụng hệ thức lượng trong tam giác vuông ⇒AB.AC=x.y⇒\(y=\dfrac{AB.AC}{x}=\dfrac{15.20}{12}=25\)

285 x X + X x 115 = 800
( 285 + 115 ) x X = 800
400 x X = 800
X = 800 : 400
X = 2
Xx(285+115)=800
Xx400=800
X=800:400
X=2
đây mà toán lớp 9 à