Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a.
\(y'=\dfrac{\left(sinx+cosx\right)'}{2\sqrt{sinx+cosx}}=\dfrac{cosx-sinx}{2\sqrt{sinx+cosx}}\)
b.
\(y'=\dfrac{-4}{\left(x-1\right)^2}\)
Tiếp tuyến vuông góc với \(y=\dfrac{1}{4}x+5\) nên có hệ số góc thỏa mãn \(k.\left(\dfrac{1}{4}\right)=-1\Rightarrow k=-4\)
\(\Rightarrow\dfrac{-4}{\left(x-1\right)^2}=-4\Rightarrow\left(x-1\right)^2=1\)
\(\Rightarrow\left[{}\begin{matrix}x=0\Rightarrow y=-3\\x=2\Rightarrow y=5\end{matrix}\right.\)
Có 2 tiếp tuyến thỏa mãn: \(\left[{}\begin{matrix}y=-4x-3\\y=-4\left(x-2\right)+5\end{matrix}\right.\)

a. \(y'\left(x_0\right)=-2x_0+3\)
b. phương trình tiếp tuyến tại x0 =2 là
\(y=y'\left(x_0\right)\left(x-x_0\right)+y_0=-\left(x-2\right)+0\text{ hay }y=-x+2\)
c.\(y_0=0\Rightarrow\orbr{\begin{cases}x_0=1\\x_0=2\end{cases}\Rightarrow PTTT\orbr{\begin{cases}y=x-1\\y=-x+2\end{cases}}}\)
d. vì tiếp tuyến vuông góc với đường thẳng có hệ số góc bằng 1 nên tiếp tuyến có hệ số góc = -1
hay \(-2x_0+3=-1\Leftrightarrow x_0=2\Rightarrow PTTT:y=-x+2\)

- Ta có : (d) : 2x – y – 3 = 0 ⇔ y = 2x - 3. Đường thẳng d có hệ số góc kd = 2 .
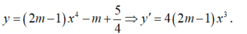
- Hệ số góc của tiếp tuyến của đồ thị hàm số 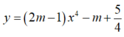 tại điểm có hoành độ x = -1 là:
tại điểm có hoành độ x = -1 là:
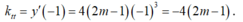
- Do tiếp tuyến vuông góc với đường thẳng d nên ta có:
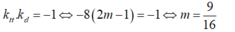
Chọn D.

Ủa hỏi mỗi hoành độ thôi hở :D?
\(f'\left(x\right)=2x-4\)
Vi \(pttt//d:y=8x+2017\Rightarrow f'\left(x\right)=8\)
\(\Rightarrow2x-4=8\Leftrightarrow x=6\)

a) + Hàm số y = cos x có chu kì 2π.
Do đó: cos 2.(x + kπ) = cos (2x + k2π) = cos 2x.
⇒ Hàm số y = cos 2x cũng tuần hoàn với chu kì π.
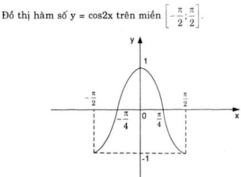
Từ đó suy ra
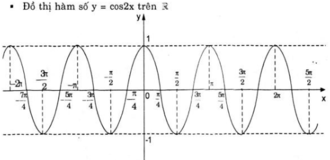
b. y = f(x) = cos 2x
⇒ y’ = f’(x) = (cos 2x)’ = -(2x)’.sin 2x = -2.sin 2x.
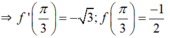
⇒ Phương trình tiếp tuyến của đồ thị (C) tại điểm có hoành độ x = π/3 là:
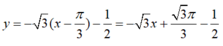
c. Ta có: 1 – cos 2x = 2.sin2x ≥ 0.
Và 1 + cos22x > 0; ∀ x
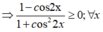
⇒ 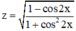 luôn xác định với mọi x ∈ R.
luôn xác định với mọi x ∈ R.
1/ a/ \(y'=-5sinx+\frac{3}{cos^2\left(x+15^0\right)}\)
b/ \(y'=\frac{6cos3x\left(-4cosx-5\right)-8sinx.sin3x}{\left(4cosx+5\right)^2}\)
2/ \(y'=-3cosx-\frac{15}{sin^23x}\Rightarrow y'\left(\frac{\pi}{4}\right)=-3cos\left(\frac{\pi}{4}\right)-\frac{15}{sin^2\left(\frac{3\pi}{4}\right)}=-\frac{60+3\sqrt{2}}{2}\)
3/ \(y'=4x-5\)
a/ \(y'\left(2\right)=3\) ; \(y\left(2\right)=2\)
Tiếp tuyến: \(y=3\left(x-2\right)+2=3x-4\)
b/ Tiếp tuyến song song \(y=2x-3\Rightarrow\) có hệ số góc bằng 2
\(\Rightarrow4x_0-5=2\Rightarrow x_0=\frac{7}{4}\Rightarrow y\left(\frac{7}{4}\right)=\frac{11}{8}\)
Tiếp tuyến: \(y=2\left(x-\frac{7}{4}\right)+\frac{11}{8}\)
c/ \(-x+3y-1=0\Rightarrow y=\frac{1}{3}x+\frac{1}{3}\)
Tiếp tuyến vuông góc với d nên có hệ số góc bằng \(-3\)
\(\Rightarrow4x_0-5=-3\Rightarrow x_0=\frac{1}{2}\Rightarrow y\left(\frac{1}{2}\right)=2\)
Tiếp tuyến: \(y=-3\left(x-\frac{1}{2}\right)+2\)
3/ a, y=\(2x^2-5x+4\)
Ta có: \(x_o=2\)-> \(y_0=2\)
-> \(f'\left(x_0\right)=3\)
Nên ta có pttt: y'= 3x - 4