Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

GIÚP MÌNH ĐI! GẤP LĂM! SÁNG 9/12/2018 LÀ MÌNH PHẢI NỘP RỒI.
A B C D M N I K E N P a) MN là dường trung bình tam giác ABD,PE là đường trung bình tam giác ACD=>MN//AD,PQ//AD=>PE//MN.
tương tự, ta có: NQ//MP. ==>MNQP laf hbh.
b) IP là đường trung bình tam giác ADC=>IP //CD, KN là đường trung bình tam giác BDC=>KN //CD, IK là đường trung bình hình thang ABCD=>IK //CD .==>NP // CD(theo tiên đề ơ-clit).
còn câu c bạn cố gắng nha, khuya quá mẹ mk bắt ngủ nên ko ghi rõ ra, phần đường trung bình là do có các trung điểm đã cho. thông cảm nha

ABCD là hbh
=>AC cắt BD tại trung điểm của mỗi đường
=>O là trung điểm chung của AC và BD
Xét ΔOAM và ΔOCP có
góc OAM=góc OCP
OA=OC
góc AOM=góc COP
=>ΔOAM=ΔOCP
=>OM=OP
=>O là trung điểm của MP
Xét ΔOQD và ΔONB có
góc ODQ=góc OBN
OD=OB
góc QOD=góc NOB
=>ΔOQD=ΔONB
=>OQ=ON
=>O là trung điểm của QN
Xét tứ giác MNPQ có
O là trung điểm chung của MP và NQ
=>MNPQ là hbh
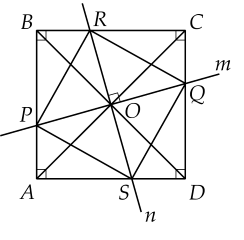
a) Ta có thể chứng minh ΔAOP = ΔBOR bằng cách sử dụng góc vuông và góc đồng quy. Vì hai đường thẳng m và n vuông góc với nhau tại O, nên góc AOP và góc BOR là góc vuông. Đồng thời, ta cũng có góc OPA = góc ORB (do OP và OR là hai cạnh của hình vuông OPRQ). Vì vậy, theo góc đồng quy, ta có ΔAOP = ΔBOR.
b) Vì O là giao điểm của hai đường chéo của hình vuông ABCD, nên ta có OP = OR = OS = OQ.
c) Ta cũng có thể chứng minh PRSQ là hình vuông bằng cách sử dụng góc vuông và góc đồng quy. Vì hai đường thẳng m và n vuông góc với nhau tại O, nên góc PQR và góc PSR là góc vuông. Đồng thời, ta cũng có góc QPR = góc RPS (do PQ và RS là hai cạnh của hình vuông PRSQ). Vì vậy, theo góc đồng quy, ta có PRSQ là hình vuông.
Vậy, ΔAOP = ΔBOR, OP = OR = OS = OQ và PRSQ là hình vuông.
sao bạn ko trình bày hẳn ra mà sao dài dòng thế