
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bạn tham khảo nhé
A=14 +116 +136 +164 +1100 +1144 +1196 =122 +142 +162 +182 +1102 +1122 +1142
2A=222 +242 +262 +282 +2102 +2122 +2142
2A<12 +22.4 +24.6 +26.8 +28.10 +210.12 +212.14
2A<12 +12 −14 +14 −16 +16 −18 +18 −110 +110 −112 +112 −114
2A<12 +12 −114
2A<1−114
2A<1314
A<1328 <1428 =12 ( đpcm )
Vậy A<12
Chúc bạn học tốt ~

1/4 = 1/(2*2) < 1/(1*2) = 1/2 - 1/4
tương tự ta có
1/16 < 1/(2*4) = 1/4 - 1/8
1/36 < 1/(4*6) = 1/8 - 1/12
1/64 < 1/(6*8) = 1/12 - 1/16
1/100 < 1/(8*10) = 1/16 - 1/20
1/144 < 1/(10*12) = 1/20 - 1/24
1/196 < 1/(12* 14) = 1/24 - 1/28
cộng hết lại
=> 1/4 + 1/16 + ......+ 1/100 + 1/144 + 1/196 < 1/2 - 1/28 < 1/2 => đpcm
ta có
1/4 = 1/(2*2) < 1/(1*2) = 1/2 - 1/4
tương tự ta có
1/16 < 1/(2*4) = 1/4 - 1/8
1/36 < 1/(4*6) = 1/8 - 1/12
1/64 < 1/(6*8) = 1/12 - 1/16
1/100 < 1/(8*10) = 1/16 - 1/20
1/144 < 1/(10*12) = 1/20 - 1/24
1/196 < 1/(12* 14) = 1/24 - 1/28
cộng hết lại
=> 1/4 + 1/16 + ......+ 1/100 + 1/144 + 1/196 < 1/2 - 1/28 < 1/2 => đpcm
Tick đúng nha bạn

khó hiểu lên thông cảm
P = 1/4 + 1/16 + 1/36 + .. + 1/196 = 1/2² + 1/4² + 1/6² +...+ 1/12² + 1/14²
xét tổng quát với số nguyên dương k ta có:
(2k-1)(2k+1) = 4k² - 1 < 4k² = (2k)² => 1/(2k)² < 1/(2k-1)(2k+1)
=> 2/(2k)² < 2 /(2k-1)(2k+1) = 1/(2k-1) - 1/(2k+1) (*)
ad (*) cho k từ 1 đến 7
2/2² < 1/1 - 1/3
2/4² < 1/3 - 1/5
...
2/12² < 1/11 - 1/13
2/14² < 1/13 - 1/15
+ + cộng lại + +
2/2² + 2/4² +...+ 2/14² < 1/1 - 1/15 < 1
=> 2(1/2² + 1/4² +..+ 1/14²) < 1 => P < 1/2 (đpcm)

ta có: \(\frac{1}{4}+\frac{1}{16}+\frac{1}{36}+\frac{1}{100}+\frac{1}{144}+\frac{1}{196}+...+\frac{1}{10000}\)
\(=\frac{1}{2^2}+\frac{1}{4^2}+\frac{1}{6^2}+\frac{1}{8^2}+\frac{1}{10^2}+\frac{1}{12^2}+\frac{1}{14^2}+...+\frac{1}{100^2}\)
Lại có: \(\frac{1}{4^2}+\frac{1}{6^2}+\frac{1}{8^2}+\frac{1}{10^2}+...+\frac{1}{100^2}< \frac{1}{2.4}+\frac{1}{4.6}+\frac{1}{6.8}+\frac{1}{8.10}+...+\frac{1}{98.100}\)
\(=\frac{1}{2}.\left(\frac{1}{2}-\frac{1}{100}\right)=\frac{1}{2}\cdot\frac{49}{100}=\frac{49}{200}\)
\(\Rightarrow\frac{1}{2^2}+\frac{1}{4^2}+\frac{1}{6^2}+\frac{1}{8^2}+\frac{1}{10^2}+...+\frac{1}{100^2}< \frac{1}{2^2}+\frac{49}{200}=\frac{99}{200}< \frac{100}{200}< \frac{1}{2}\)
=> đ p c m


hình như phân số cuối phải là 1/324
nếu là 1/324 thì tớ giải nè:
A = 1/4+1/16+1/36+1/64+1/100+1/144+1/196+1/256+1/324
= 1/4.(1+1/2^2+1/3^2+1/4^2+1/5^2+1/6^2+1/7^2+1/8^2+1/9^2) <1/4.(1+1/1.2+1/2.3+1/3.4+1/4.5+1/5.6+1/6.7+1/7.8+1/8.9)
= 1/4.(1+1-1/9)
= 1/4.17/9 = 17/36<18/36 = 1/2
=> A = 1/4+1/16+1/36+1/64+1/100+1/144+1/196+1/256+1/324<1/2


A = 1/4+1/16+1/36+1/64+1/100+1/144+1/196+1/256+1/324
= 1/4.(1+1/2^2+1/3^2+1/4^2+1/5^2+1/6^2+1/7^2+1/8^2+1/9^2) <1/4.(1+1/1.2+1/2.3+1/3.4+1/4.5+1/5.6+1/6.7+1/7.8+1/8.9)
= 1/4.(1+1-1/9)
= 1/4.17/9 = 17/36<18/36 = 1/2
=> A = 1/4+1/16+1/36+1/64+1/100+1/144+1/196+1/256+1/324<1/2
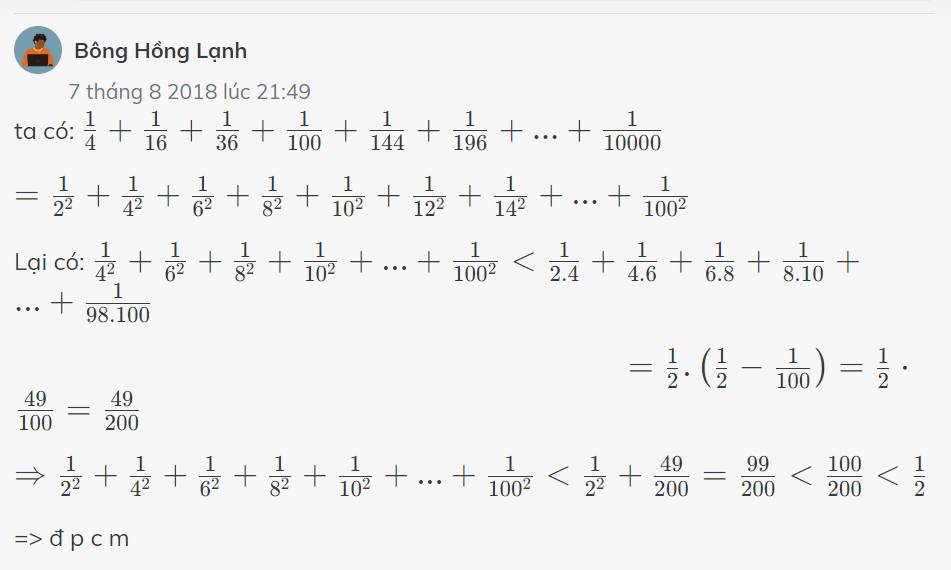
1/144 PHẢI ĐỔI THÀNH 1/100 MỚI ĐÚNG HƠN. BẠN XEM LẠI ĐỀ BÀI XEM
\(A< \frac{1}{1.3}+\frac{1}{3.5}+\frac{1}{5.7}+\frac{1}{7.9}+\frac{1}{9.11}+\frac{1}{11.13}+\frac{1}{13.15}.\)
\(2A< \frac{2}{1.3}+\frac{2}{3.5}+\frac{2}{5.7}+\frac{2}{7.9}+\frac{2}{9.11}+\frac{2}{11.13}+\frac{2}{13.15}\)
\(2A< \frac{3-1}{1.3}+\frac{5-3}{3.5}+\frac{7-5}{5.7}+\frac{9-7}{7.9}+\frac{11-9}{9.11}+\frac{13-11}{11.13}+\frac{15-13}{13.15}\)
\(2A< 1-\frac{1}{3}+\frac{1}{3}-\frac{1}{5}+\frac{1}{5}-\frac{1}{7}+...+\frac{1}{13}-\frac{1}{15}=1-\frac{1}{15}< 1\)
\(\Rightarrow2A< 1\Rightarrow A< \frac{1}{2}\)