K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NG
13
HN
10 tháng 5 2018
M∈ (S) : (x0 - 2)2 + (y0-1)2 +(z0-1)2 =9.
A=x0+2y0+2z0=(x0-2)+2(y0-1)+2(z0-1)+6
Dùng BĐT bunhiacopski
[(x0-2)+2(y0-1)+2(z0-1)]2 ≤ (1+4+4).[(x0 - 2)2 + (y0-1)2 +(z0-1)2 ]
≤ 81
-9 ≤ (x0-2)+2(y0-1)+2(z0-1) ≤ 9.
-3 ≤ A ≤ 12. vậy GTNN của A = -3.
Dấu bằng xảy ra khi :
x0+2y0+2z0 = -3
và \(\dfrac{x0-2}{1}=\dfrac{y0-1}{1}=\dfrac{z0-1}{1}\)
Giải hệ được x0=1, y0=z0=-1. Suy ra: x0+y0+z0 = -1
MW
0
LN
0
LV
8 tháng 2 2017
Ta có : \(5^{2x}-24.5^{x-1}-1=0\Leftrightarrow5^{2x}-\frac{24}{5}.5^x-1=0\)
Đặt \(t=5^x,\left(t>0\right)\)
a)Phương trở thành : \(\Leftrightarrow t^2-\frac{24}{5}.t-1=0\left[\begin{matrix}t=5\\t=-\frac{1}{5}\left(l\right)\end{matrix}\right.\)
Với \(t=5\) ta có \(x=1\)
Vậy phương trình có nghiệm là : \(x=1\) và \(x=-1\)
ĐK: \(x>1\)
b)Ta có phương trình :\(\Leftrightarrow log_{\frac{1}{2}}+log_{\frac{1}{2}}\left(x-1\right)+log_26=0\Leftrightarrow log_{\frac{1}{2}}x\left(x-1\right)+log_26=0\)
\(\Leftrightarrow log_2x\left(x-1\right)=log_26\)
\(\Leftrightarrow x\left(x-1\right)=6\Leftrightarrow\left[\begin{matrix}x=3\\x=-2\end{matrix}\right.\)
Đôi chiếu điều kiện ta thấy phương trình có nghiệm \(x=3\)
NP
1
NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 5 2020
Hệ vecto đã cho độc lập tuyến tính
Đặt \(\left\{{}\begin{matrix}x_1=\left(1;0;1\right)\\x_2=\left(1;-1;1\right)\\x_3=\left(1;2;0\right)\end{matrix}\right.\)
Chọn \(y_1=x_1\)
Chọn \(y_2=x_2+tx_1\) với \(t=-\frac{< x_2;y_1>}{< y_1;y_1>}=-\frac{1.1+0.\left(-1\right)+1.1}{1^2+0^2+1^2}=-1\)
\(\Rightarrow y_2=\left(1;-1;1\right)+\left(-1;0;-1\right)=\left(0;-1;0\right)\)
Chọn \(y_3=x_3+t_1y_1+t_2y_2\) với:
\(t_1=-\frac{< x_3;y_1>}{< y_1;y_1>}=-\frac{1.1+0.2+1.0}{1^2+0^2+1^2}=-\frac{1}{2}\)
\(t_2=-\frac{< x_3;y_2>}{< y_2;y_2>}=-\frac{1.0+2.\left(-1\right)+0.0}{0^2+\left(-1\right)^2+0^2}=-\frac{-2}{1}=2\)
\(\Rightarrow y_3=\left(1;2;0\right)+\left(-\frac{1}{2};0;-\frac{1}{2}\right)+\left(0;-2;0\right)=\left(\frac{1}{2};0;-\frac{1}{2}\right)\)
Vậy ta có hệ trực giao: \(\left\{{}\begin{matrix}y_1=\left(1;0;1\right)\\y_2=\left(0;-1;0\right)\\y_3=\left(\frac{1}{2};0;-\frac{1}{2}\right)\end{matrix}\right.\)
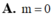
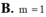
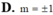
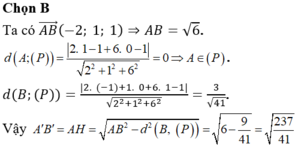
1/0 ( chắc thé )
TL: 1:0= Lỗi nhé bn