Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
\(\overrightarrow{NM}=\left(4;-2;2\right)=2\left(2;-1;1\right)\)
Gọi Q là trung điểm MN \(\Rightarrow Q\left(-1;3;2\right)\)
Phương trình mặt phẳng trung trực của MN (đi qua Q và nhận \(\overrightarrow{NM}\) là 1 vecto pháp tuyến) có dạng:
\(2\left(x+1\right)-1\left(y-3\right)+1\left(z-2\right)=0\)
\(\Leftrightarrow2x-y+z+3=0\)
b.
(P) có 1 vecto pháp tuyến là \(\left(1;2;-1\right)\)
Do \(\left(\beta\right)\) song song (P) nên cũng nhận \(\left(1;2;-1\right)\) là 1 vtpt
À thôi bạn ghi sai đề rồi, \(\left(\beta\right)\) chỉ có thể đi qua M hoặc N (1 điểm thôi), không thể đi qua MN được vì MN không song song với (P)
Có hai trường hợp xảy ra:
Trường hợp 1:
(P) đi qua A, song song với hai đường thẳng d và BC. Vectơ chỉ phương của d là v → (-3; -1; 2) và BC → (-2; 4; 0).
Do đó n P → = v → ∧ BC → = (-8; -4; -14).
Phương trình mặt phẳng (P) là: -8(x - 1) - 4(y - 2) - 14(z - 1) = 0 hay 4x + 2y + 7z - 15 = 0
Trường hợp 2:
(P) đi qua A, đi qua trung điểm F(1; 1; 1) của BC, và song song với d.
Ta có: FA → (0; 1; 0), FA → ∧ v → = (2; 0; 3).
Suy ra phương trình của (P) là: 2(x - 1) + 3(z - 1) = 0 hay 2x + 3z - 5 = 0.
Bài 1.
a) \(\left(3+4i\right)+\left(-1+5i\right)=\left(3-1\right)+\left(4i+5i\right)=2+9i\)
b) \(\left(3-4i\right)-\left(1-5i\right)=\left(3-1\right)-\left(4i-5i\right)=2+i\)
c)\(\left(-3+4i\right)+\left(1-4i\right)=\left(-3+1\right)+\left(4i-4i\right)=-2\)
d) \(\left(3-5i\right)-\left(4+i\right)=\left(3-4\right)-\left(5i+i\right)=-1-6i\)
Bài 2.
a) \(\left(3+4i\right)\left(-1+5i\right)=3.\left(-1\right)+4i.\left(-1\right)+3.5i+4i.5i\)
\(=-3-4i+15i-20=-23+11i\)
b) \(\left(3-5i\right)-\left(4+i\right)=\left(3-4\right)-\left(5i+i\right)=-1-6i\)
Chọn A
Ta có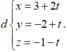 
Vì M là giao điểmcủa d và (P) nên ta có tọa độ của M cũng thỏa mãn phương trình mặt phẳng (P) hay
Gọi điểm H là hình chiếu của M lên
đường thẳng ∆ ta có
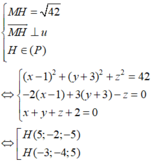
Vậy tồn tại hai đường thẳng ∆ thỏa mãn đề bài
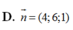
Hệ vecto đã cho độc lập tuyến tính
Đặt \(\left\{{}\begin{matrix}x_1=\left(1;0;1\right)\\x_2=\left(1;-1;1\right)\\x_3=\left(1;2;0\right)\end{matrix}\right.\)
Chọn \(y_1=x_1\)
Chọn \(y_2=x_2+tx_1\) với \(t=-\frac{< x_2;y_1>}{< y_1;y_1>}=-\frac{1.1+0.\left(-1\right)+1.1}{1^2+0^2+1^2}=-1\)
\(\Rightarrow y_2=\left(1;-1;1\right)+\left(-1;0;-1\right)=\left(0;-1;0\right)\)
Chọn \(y_3=x_3+t_1y_1+t_2y_2\) với:
\(t_1=-\frac{< x_3;y_1>}{< y_1;y_1>}=-\frac{1.1+0.2+1.0}{1^2+0^2+1^2}=-\frac{1}{2}\)
\(t_2=-\frac{< x_3;y_2>}{< y_2;y_2>}=-\frac{1.0+2.\left(-1\right)+0.0}{0^2+\left(-1\right)^2+0^2}=-\frac{-2}{1}=2\)
\(\Rightarrow y_3=\left(1;2;0\right)+\left(-\frac{1}{2};0;-\frac{1}{2}\right)+\left(0;-2;0\right)=\left(\frac{1}{2};0;-\frac{1}{2}\right)\)
Vậy ta có hệ trực giao: \(\left\{{}\begin{matrix}y_1=\left(1;0;1\right)\\y_2=\left(0;-1;0\right)\\y_3=\left(\frac{1}{2};0;-\frac{1}{2}\right)\end{matrix}\right.\)
Cảm ơn b nhé