Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

câu 1 là :từ a/x + b/y + c/z =0 suy ra (ayz+bxz+cxy)/xyz =0 suy ra ayz+bxz+cxy=0 (1)
vì x/a + y/b + z/c =1 (gt) suy ra (x/a + y/b + z/c )^2 = 1^2 . suy ra x^2/a^2 + y^2/b^2 + z^2/c^2 + 2(xy/ab + yz/bc + xz/ac) =1
suy ra x^2/a^2 + y^2/b^2 + z^2/c^2 + 2[(ayz+bxz+cxy)/abc = 1 (2)
Từ (1) và (2) suy ra x^2/a^2 + y^2/b^2 + z^2/c^2 =1 (đpcm)

Có: \(\frac{a}{x}+\frac{b}{y}+\frac{c}{z}=0\)
\(\Leftrightarrow\frac{ayz+bxz+cxy}{xyz}=0\)
\(\Leftrightarrow ayz+bxz+cxy=0\)
Lại có: \(\frac{x}{a}+\frac{y}{b}+\frac{z}{c}=1\)
\(\Leftrightarrow\frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{c^2}+2\left(\frac{xy}{ab}+\frac{yz}{bc}+\frac{xz}{ac}\right)=1\)
\(\Leftrightarrow\frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{c^2}=1-2\left(\frac{xy}{ab}+\frac{yz}{bc}+\frac{xz}{ac}\right)=1-2\cdot\frac{ayz+bxz+cxy}{abc}=1-2\cdot\frac{0}{abc}=1\)
=>đpcm

a: x-y-z=0
=>x=y+z; y=x-z; z=x-y
\(K=\dfrac{x-z}{x}\cdot\dfrac{y-x}{y}\cdot\dfrac{z+y}{z}=\dfrac{y\cdot\left(-z\right)\cdot x}{xyz}=-1\)
b: Tham khảo:
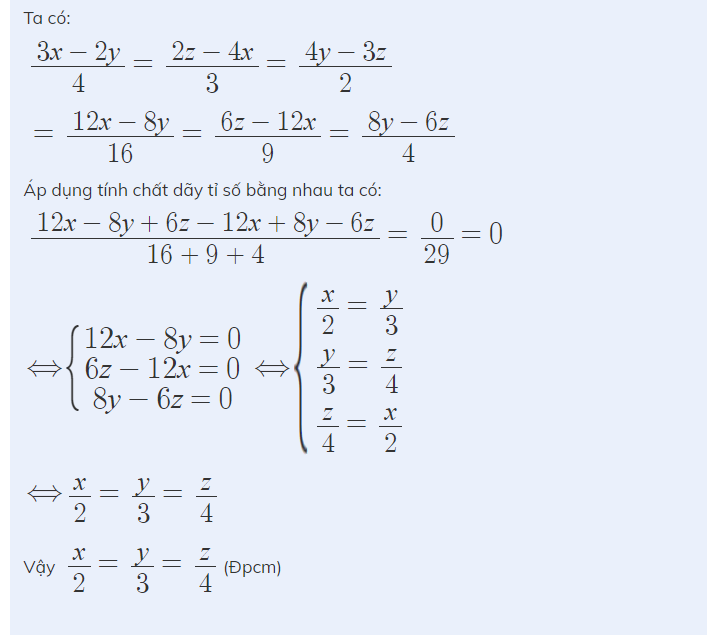
Lạ nhỉ mình trả lời rồi mà
ta có {nhân phân phối ra dẽ hơn} là ghép nhân tử
\(\left(\frac{x}{y+z}+\frac{y}{z+x}+\frac{z}{x+y}\right)\left(x+y+z\right)=\left(\frac{x^2}{y+z}+\frac{y^2}{z+x}+\frac{z^2}{x+y}....\right)+\left(x+y+z\right)\)
Chia hai vế cho (x+y+z khác 0) chú ý => dpcm
quái lại câu 1 đâu
(a+b+c)=abc tất nhiên theo đầu đk a,b,c khác không
chia hai vế cho abc/2
2/bc+2/ac+2/ab=2 (*)
đăt: 1/a=x; 1/b=y; 1/c=z
ta có
x+y+z=k (**)
x^2+y^2+z^2=k(***)
lấy (*)+(***),<=>(x+y+z)^2=2+k
=> k^2=2+k
=> k^2-k=2
k^2-k+1/4=1/4+2=9/4
\(\orbr{\begin{cases}k=\frac{1}{2}+\frac{3}{2}=\frac{5}{2}\\k=\frac{1}{2}-\frac{3}{2}=-\frac{1}{2}\end{cases}}\)
Mình chưa test lại đâu bạn tự test nhé