Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

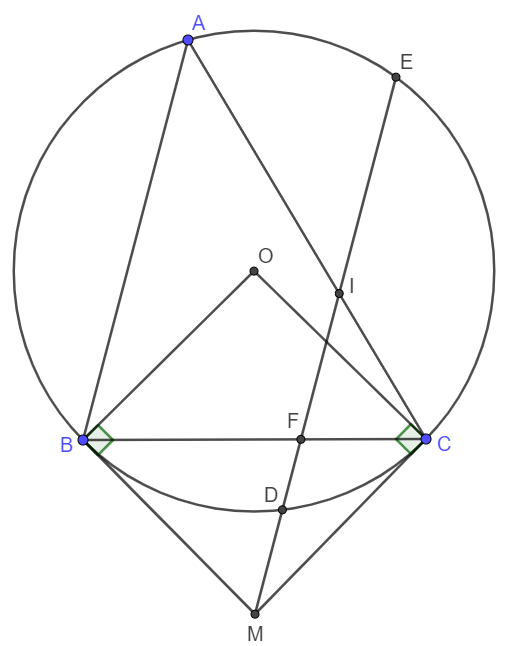
Cho tam giác ABCABC không có góc tù (AB < AC)(AB<AC), nội tiếp đường tròn (O; R)(O;R), (BB, CC cố định, AA di động trên cung lớn BC). Các tiếp tuyến tại BB và CC cắt nhau tại MM. Từ MM kẻ đường thẳng song song với ABAB, đường thẳng này cắt (O)(O) tại DD và EE (DD thuộc cung nhỏ BCBC), cắt BCBC tại FF, cắt ACAC tại II. Chứng minh rằng \widehat{MBC}=\widehat{BAC}MBC=BAC . Từ đó suy ra MBICMBIC là tứ giác nội tiếp.
theo gt, ta co:
goc MBC= BAC (cung chan cung BC)
mat khac, ta lai co goc BAC = MIC ( dong vi)
=> goc MBC= MIC
=> tu giac BICM noi tiep

Lời giải:

a)
Vì $AF$ là tiếp tuyến của $(O)$ nên \(AF\perp OF\) hay \(DA\perp OF\Rightarrow \widehat{DFO}=90^0\)
$DB$ là tiếp tuyến của $(O)$ nên \(DB\perp OB\Rightarrow \widehat{DBO}=90^0\)
Tứ giác $DBOF$ có tổng hai góc đối nhau
\(\widehat{DFO}+\widehat{DBO}=90^0+90^0=180^0\) nên là tứ giác nội tiếp.
b)
Áp dụng định lý Pitago cho tam giác $OFA$ vuông tại $F$:
\(OA=\sqrt{OF^2+FA^2}=\sqrt{R^2+(\frac{4}{3}R)^2}=\frac{5}{3}R\)
Ta có:
\(\cos \widehat{DAB}=\cos \widehat{OAF}=\frac{FA}{OA}=\frac{\frac{4}{3}R}{\frac{5}{3}R}=\frac{4}{5}\)
c) \(OM\perp BA, BD\perp BA\Rightarrow OM\parallel BD\)
Theo tính chất hai đường tiếp tuyến cắt nhau suy ra $DO$ là phân giác góc \(\widehat{BDF}\)
\(\Rightarrow \widehat{BDO}=\widehat{ODM}\)
Mà \(OM\parallel BD\Rightarrow \widehat{MOD}=\widehat{ODB}\) (so le trong)
Suy ra \(\widehat{ODM}=\widehat{MOD}\Rightarrow \triangle MDO\) cân tại $M$
\(\Rightarrow MD=MO\)
Áp dụng định lý Thales với \(MO\parallel DB\) ta có:
\(\frac{DA}{MA}=\frac{DB}{MO}=\frac{DB}{DM}\)
\(\Leftrightarrow \frac{DM+MA}{MA}=\frac{DB}{DM}\Rightarrow \frac{BD}{DM}-\frac{DM}{AM}=1\) (đpcm)
1. Cho nửa đtr tâm O đường kính AB. M bất kì thuộc cung AB. MD ⊥AB. Qua C ∈cung MB kẻ tiếp tuyến Cx cắt DM tại I. DM cắt AC ở E, BC tại F. Chứng minh
a) B,C,E,D thuộc 1 đtr
A,D,C,F thuộc 1 đtr
b) ^MEC=^ABC
c) I là tâm đtr ngoại tiếp tam giác EFC