Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

2) b)
Do \(a+b+c=9\Rightarrow\left(a+b+c\right)^2=81\)
\(\Rightarrow a^2+b^2+c^2+2\left(ab+bc+ac\right)=81\)
\(\Rightarrow2\left(ab+bc+ac\right)=81-141=-60\)
\(ab+bc+ac=-60:2=-30\)
a, B=x^3 + 3xy +y^3 = x^3 +3xy(x+y)+y^3 (vì x+y=1)
= (x+y)^3
= 1^3 =1
b, (a+b+c)^2 =a^2 +b^2 +c^2 +2ab +2bc +2ac
9^2 = 141 +2(ab+bc+ac)
-60 = 2(ab+bc+ac)
ab+ac+bc=-30
Vậy M=-30
c, N =(x+y)^3 -3(x+y)(x^2+y^2) +2(x^3+y^3)
= x^3 + 3x^2 .y + 3xy^2 + -3(x^3+xy^2 +x^2 .y+y^3)+ 2x^3 +2y^3
= x^3 +3x^2 .y + 3xy^2 - 3x^3 -3xy^2 -3x^2 .y -3y^3 +2x^3 +2y^3
= 0
Vậy N=0 .Chúc bạn học tốt.

b; 13 = (\(x-y\))3 = \(x^3\) - 3\(x^2\).y + 3\(xy^2\) - y3 = \(x^3\) - y3 - 3\(xy\)(\(x-y\))
1 = \(x^3\) - y3 - 3\(xy\)

1/ Ta có : P\left(x\right)=-x^2+13x+2012=-\left(x-\frac{13}{2}\right)^2+\frac{8217}{4}\le\frac{8217}{4}P(x)=−x2+13x+2012=−(x−213)2+48217≤48217
Dấu "=" xảy ra khi x = 13/2
Vậy Max P(x) = 8217/4 tại x = 13/2
1/ Ta có : P\left(x\right)=-x^2+13x+2012=-\left(x-\frac{13}{2}\right)^2+\frac{8217}{4}\le\frac{8217}{4}P(x)=−x2+13x+2012=−(x−213)2+48217≤48217
Dấu "=" xảy ra khi x = 13/2
Vậy Max P(x) = 8217/4 tại x = 13/2
2/ Ta có : x^3+3xy+y^3=x^3+3xy.1+y^3=x^3+y^3+3xy\left(x+y\right)=\left(x+y\right)^3=1x3+3xy+y3=x3+3xy.1+y3=x3+y3+3xy(x+y)=(x+y)3=1
3/ a+b+c=0\Leftrightarrow\left(a+b+c\right)^2=0\Leftrightarrow a^2+b^2+c^2+2\left(ab+bc+ac\right)=0a+b+c=0⇔(a+b+c)2=0⇔a2+b2+c2+2(ab+bc+ac)=0
\Leftrightarrow ab+bc+ac=-\frac{1}{2}⇔ab+bc+ac=−21 \Leftrightarrow\left(ab+bc+ac\right)^2=\frac{1}{4}\Leftrightarrow a^2b^2+b^2c^2+c^2a^2+2abc\left(a+b+c\right)=\frac{1}{4}⇔(ab+bc+ac)2=41⇔a2b2+b2c2+c2a2+2abc(a+b+c)=41
\Leftrightarrow a^2b^2+b^2c^2+c^2a^2=\frac{1}{4}⇔a2b2+b2c2+c2a2=41(vì a+b+c=0)
Ta có : a^2+b^2+c^2=1\Leftrightarrow\left(a^2+b^2+c^2\right)^2=1\Leftrightarrow a^4+b^4+c^4+2\left(a^2b^2+b^2c^2+c^2a^2\right)=1a2+b2+c2=1⇔(a2+b2+c2)2=1⇔a4+b4+c4+2(a2b2+b2c2+c2a2)=1
\Leftrightarrow a^4+b^4+c^4=1-2\left(a^2b^2+b^2c^2+c^2a^2\right)=1-\frac{2.1}{4}=\frac{1}{2}⇔a4+b4+c4=1−2(a2b2+b2c2+c2a2)=1−42.1=21

a. Có \(x+y=2\Rightarrow x^2+2xy+y^2=4\Rightarrow x^2+y^2=4-2.\left(-3\right)=10\)
\(x^4+y^4=\left(x^2\right)^2+\left(y^2\right)^2=\left(x^2+y^2\right)^2-2x^2y^2\)
\(=10^2-2.\left(-3\right)^2=82\)
b. Ta có \(x+y=1\Rightarrow x^2+y^2=1-2xy\)
\(x^3+y^3+3xy=\left(x+y\right)\left(x^2-xy+y^2\right)+3xy\)
\(=1.\left(1-2xy-xy\right)+3xy=1\)
Các câu còn lại tương tự

1/ \(a+b+c=11\)
\(\Leftrightarrow a^2+b^2+c^2+2\left(ab+bc+ca\right)=121\)
\(\Leftrightarrow ab+bc+ca=\frac{121-\left(a^2+b^2+c^2\right)}{2}=\frac{121-87}{2}=17\)
2/ \(a^3+b^3+a^2c+b^2c-abc\)
\(=\left(a+b\right)\left(a^2-ab+b^2\right)+c\left(a^2-ab+b^2\right)\)
\(=\left(a^2-ab+b^2\right)\left(a+b+c\right)=0\)
3/ \(x^4+3x^3y+3xy^3+y^4\)
\(=\left(\left(x+y\right)^2-2xy\right)^2-2x^2y^2+3xy\left(\left(x+y\right)^2-2xy\right)\)
\(=\left(9^2-2.4\right)^2-2.4^2+3.4.\left(9^2-2.4\right)=6173\)
bạn alibaba nguyễn có thể làm lại giúp mình được không ?

1, \(A=x^3+y^3+3xy\)
\(=x^3+3x^2y+3xy^2+y^2+3xy-3x^2y-3xy^2\)
\(=\left(x+y\right)^3+3xy-3xy\left(x+y\right)\)
Thay x +1 = 1 ta có
\(1^3+3xy-3xy.1=1+3xy-3xy=1\)

\(a)\)\(M=x^3-3xy\left(x-y\right)-y^3-x^2+2xy-y^2\) ( đề nhầm đúng ko bn )
\(M=\left(x^3-3x^2y+3xy^2-y^3\right)-\left(x^2-2xy+y^2\right)\)
\(M=\left(x-y\right)^3-\left(x-y\right)^2\)
\(M=7^3-7^2\)
\(M=294\)
Chúc bạn học tốt ~

1/Ta có: \(\left(a+b+c\right)^2=a^2+b^2+c^2+2\left(ab+bc+ca\right)=81\)
\(\Rightarrow M=ab+bc+ca=\frac{\left(81-141\right)}{2}\)
bài 1
bài 2
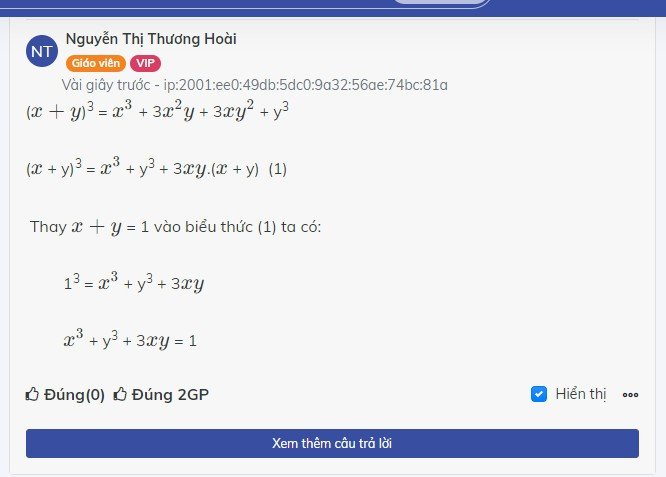
ta có: \(\left(x+y\right)^3=x^3+y^3+3x^2y+3xy^2\)
\(\Leftrightarrow\)\(\left(x+y\right)^3=x^3+y^3+3xy\left(x+y\right)\)
mà x+y=1 nên
1=\(x^3+y^3+3xy.1\)
Vậy =1
\(2;x^3+y^3+3xy\)
\(=\left(x+y\right)\left(x^2-xy+y^2\right)+3xy\)
\(=x^2-xy+y^3+3xy\)
\(=\left(x+y\right)^2=1\)
\(1;\left(a+b+c\right)^3=0\)
\(\Rightarrow\left[\left(a+b\right)+c\right]^3=0\)
\(\Rightarrow\left(a+b\right)^3+3.\left(a+b\right)^2.c+3\left(a+b\right).c^2+c^3=0\)
\(\Rightarrow a^3+3a^2b+3ab^2+b^3+3\left(a^2+2ab+b^2\right)c+3ac^2+3bc^2+c^3=0\)
\(\Rightarrow\left(a^3+b^3+c^3\right)+3a^2b+3ab^2+3a^2c+6abc+3b^2c+3ac^2+3bc^2=0\)