Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vectơ trong không gian là một đoạn thẳng có định hướng, tức là một đoạn thẳng đã được chỉ rõ điểm đầu và điểm cuối.
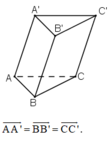

Đáp án D.
Gọi M là trung điểm BC, dựng ![]()
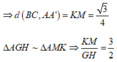
![]()
∆ AA'G vuông tại G, GH là đường cao => A'G = 1 3
Vậy 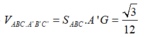

a.
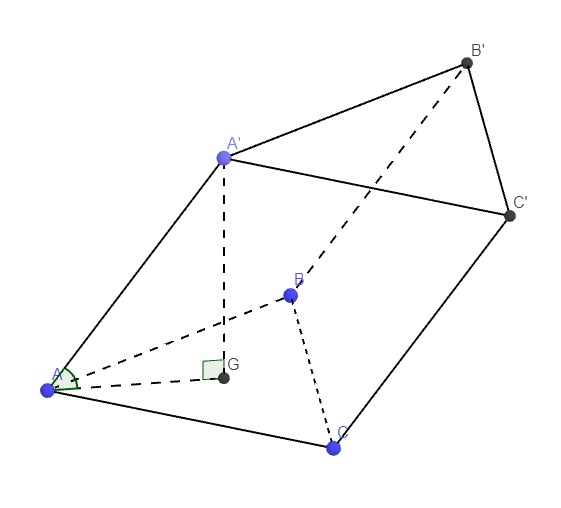
Do A' cách đều A,B,C \(\Rightarrow A'A=A'B=A'C\) hay \(A'ABC\) là chóp tam giác đều
\(\Rightarrow\) Hình chiếu vuông góc của A' lên (ABC) trùng trọng tâm ABC
Gọi G là trọng tâm ABC \(\Rightarrow A'G\perp\left(ABC\right)\)
\(\Rightarrow A'G\) là đường cao lăng trụ
Lại có \(A'G\perp\left(ABC\right)\Rightarrow AG\) là hình chiếu vuông góc của A'A lên (ABC)
\(\Rightarrow\widehat{A'AG}\) là góc giữa A'A và (ABC) \(\Rightarrow\widehat{A'AG}=60^0\)
\(AG=\dfrac{2}{3}.\dfrac{a\sqrt{3}}{2}=\dfrac{a\sqrt{3}}{3}\Rightarrow A'G=AG.tan60^0=a\)
b.
Đề bài thật kì quặc, ở giả thiết đã cho sẵn góc giữa A'A và (ABC) là 60 độ sao còn bắt tính?
Còn góc đó chúng ta đã xác định ở câu a là \(\widehat{A'AG}\)

Đáp án C
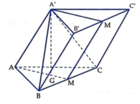
Ta dễ dàng chứng minh được AA'//(BCC'B')
![]()
![]()
Gọi G là trọng tâm của tam giác ABC. Suy ra A'G ⊥ (ABC)
Ta có
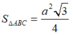
![]()
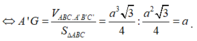
Lại có
![]()
![]()
Ta luôn có
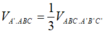
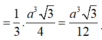
![]()
![]()

Gọi M, M' lần lượt là trung điểm của BC và B'C'. Ta có ![]() .
.![]()
Mà MM'//BB' nên BC ⊥ BB' => BCC'B' là hình chữ nhật
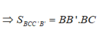
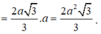
Từ:
![]()
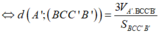
![]()
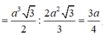
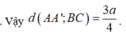

Một vectơ khác vectơ không được xác định bởi 2 điểm phân biệt.
Từ 4 điểm ban đầu ta có 4 cách chọn điểm đầu và 3 cách chọn điểm cuối.
Do đó; có tất cả 4.3= 12 vecto được tạo ra.
Chọn D

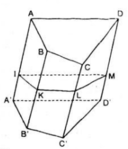

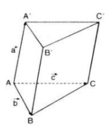
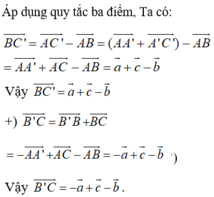
Vectơ trong không gian là một đoạn thẳng có định hướng, tức là một đoạn thẳng đã được chỉ rõ điểm đầu và điểm cuối.
Vì các cạnh bên của hình lăng trụ là các đoạn thẳng song song và bằng nhau nên các vectơ bằng vectơ và có điểm đầu và điểm cuối là đỉnh của hình lăng trụ là: các vector BB', CC', DD'.