Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D.
Gọi P 1 , P 2 là công suất nguồn phát, P t là công suất nơi tiêu thụ.
Do công suất nới tiêu thụ không đổi nên ta có: ![]() (1)
(1)
Lại có: 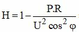
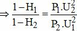
Từ (1) và (2) 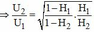
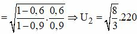
![]()

Đáp án: C
+ H2/H1 = Pt2/P2 . P1/Pt1 = U1I1/U2I2 = I1/4I2 (1)
+ Pt .( 1 H - 1 ) = DP →I12/I22 = 1 H 1 - 1 1 H 2 - 1 → I1/I2 = H 2 H 1 1 - H 1 1 - H 2 (2)
Từ (1) và (2) → 16 H 2 H 1 = 1 - H 1 1 - H 2 → H2 = 0,99 = 99%.

@nguyễn mạnh tuấn Bạn làm đúng rồi nhé, mình không thấy sai đâu cả.

Đáp án C
+ Với công suất nơi tiêu thụ là không đổi, để thay đổi hiệu suất của quá trình truyền tải, rõ ràng công suất nơi phát phải thay đổi.
Gọi ∆ P 1 và ∆ P 2 lần lượt là hao phí truyền tải tương ứng với hai trường hợp
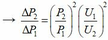 hay
hay 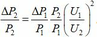
+ Với 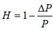 Ta có
Ta có 
mặc khác
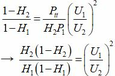
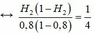
![]()

Đáp án C
+ Với công suất nơi tiêu thụ là không đổi, để thay đổi hiệu suất của quá trình truyền tải, rõ ràng công suất nơi phát phải thay đổi.
Gọi ∆ P 1 và ∆ P 2 lần lượt là hao phí truyền tải tương ứng với hai trường hợp
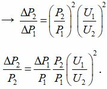
+ Với ![]() Ta có
Ta có 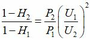
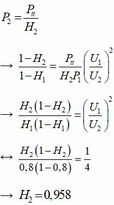

Đáp án C
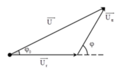
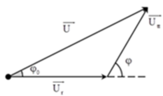
+ Ta có giản đồ vecto cho các điện áp
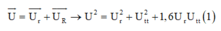
+ Mặc khác kết hợp với giả thuyết
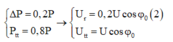
+ Thay hệ trên vào (1) ta tìm được cos φ = 5 34
+ Để giảm hao phí xuống 4 lần, nghĩa là I giảm 2 lần do vậy U r = I r cũng giảm đi hai lần
![]()
+Áp dụng định lý sin trong tam giác
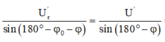
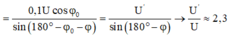

Giải thích: Đáp án A
Phương pháp:Sử dụng giản đồ vecto
Công thức tính công suất và hiệu suất
Lí thuyết về truyền tải điện năng đi xa
Cách giải: Ta có: cosφ' = 0,8
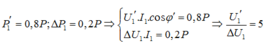
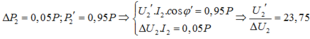
Sử dụng định lí hàm số cos:
![]()
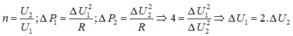
Chuẩn hoá số liệu: Cho ∆U1 = 1 => U1’ = 5


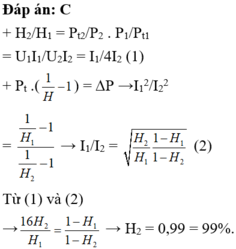


Công suất hap phí trong quá trình truyền đi là \(\Delta P = I^2R = \frac{P^2}{U^2}R\)
Hiệu suất: \(H = \frac{P_{ich}}{P} = \frac{P-\Delta P}{P} = 1 - \frac{\Delta P }{P} = 1 - \frac{P}{U^2}R\)
\(U_1 = 220:\) \(0,6 = 1- \frac{P}{U_1^2}R => \frac{P}{U_1^2}R = 0,4.(1)\)
\(U_2\): \(0,9 = 1- \frac{P}{U_2^2}R => \frac{P}{U_2^2}R = 0,1.(2)\) (do P = const; R = const)
Lập tỉ số \((1), (2)\) =>\(\frac{U_2^2}{U_1^2} = 4\)
=> \(U_2 = 2U_1 = 2.220 = 440V.\)
Chọn đáp án.D.467V