Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
+ Với công suất nơi tiêu thụ là không đổi, để thay đổi hiệu suất của quá trình truyền tải, rõ ràng công suất nơi phát phải thay đổi.
Gọi ∆ P 1 và ∆ P 2 lần lượt là hao phí truyền tải tương ứng với hai trường hợp
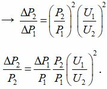
+ Với ![]() Ta có
Ta có 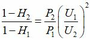
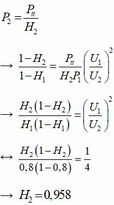

Chọn đáp án A
+ Khi chưa tăng công suất nơi tiêu thụ ta có: ![]() với
với ![]()
+ Khi tăng công suất nơi tiêu thụ lên 10% ta có:
![]()
![]()
+ Lập tỉ số 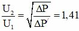

Giải thích: Đáp án B
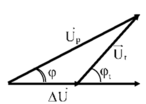
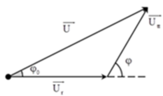
Từ giản đồ vectơ ta có
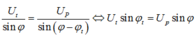
![]()
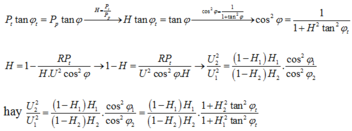
*Áp dụng công thức:
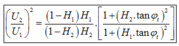
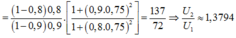

Chọn D.
Gọi P 1 , P 2 là công suất nguồn phát, P t là công suất nơi tiêu thụ.
Do công suất nới tiêu thụ không đổi nên ta có: ![]() (1)
(1)
Lại có: 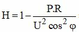
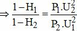
Từ (1) và (2) 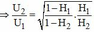
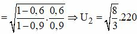
![]()

Đáp án C
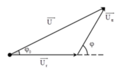
+ Ta có giản đồ vecto cho các điện áp
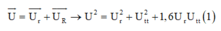
+ Mặc khác kết hợp với giả thuyết
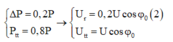
+ Thay hệ trên vào (1) ta tìm được cos φ = 5 34
+ Để giảm hao phí xuống 4 lần, nghĩa là I giảm 2 lần do vậy U r = I r cũng giảm đi hai lần
![]()
+Áp dụng định lý sin trong tam giác
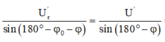
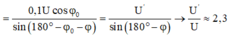

Giải thích: Đáp án A
Phương pháp:Sử dụng giản đồ vecto
Công thức tính công suất và hiệu suất
Lí thuyết về truyền tải điện năng đi xa
Cách giải: Ta có: cosφ' = 0,8
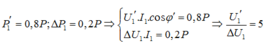
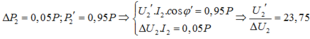
Sử dụng định lí hàm số cos:
![]()
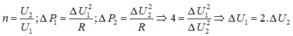
Chuẩn hoá số liệu: Cho ∆U1 = 1 => U1’ = 5


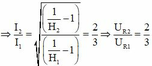
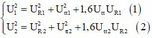
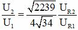
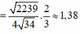


Đáp án C
+ Với công suất nơi tiêu thụ là không đổi, để thay đổi hiệu suất của quá trình truyền tải, rõ ràng công suất nơi phát phải thay đổi.
Gọi ∆ P 1 và ∆ P 2 lần lượt là hao phí truyền tải tương ứng với hai trường hợp
+ Với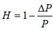 Ta có
Ta có 
mặc khác